Competitive Programming Editorial & Misc Articles
競技プログラミングの解説記事やその他いろいろなことについて書いています。
重要: 旧ブログからの移植作業を完了しました!ただ、数式やレイアウト等が壊れている可能性があります。
もし変な場所がある場合は DM かなにかでご一報ください。
問題リンク
https://yukicoder.me/problems/no/1313
問題概要
先攻のプレイヤーであるあなたは $0$ から始めます。交互に $[1,\ K]$ のうちのどれかの整数を加算していきます。$N$ 以上の数字、または予め指定された危険な数字を言ってしまうと負けです。
あなたが勝つ場合は最初に宣言して勝てる数字を全て出力してください。あなたが負ける場合は $0$ を出力してください。
制約
- $N,\ K$ は整数
- $1\le K\lt N\le 2\times 10^{5}$
- $|S|=N-1$
- $S_{i}$ が
xのときは $i$ は「危険な数字」で、oのときはそうではない
これから私が yukicoder において Writer/Tester をした問題やコンテストの講評は開催されるたびに上げようと思います。当然ですが、問題のネタバレを含みます。
私の Writer をした問題では初出題です。yukicoder 毎年恒例のアドカレコンのうち 1 問を担当させて頂きました。色々不慣れな点もありましたが無事出題でき、良かったです。Tester のりあんさんには感謝です!
yukicoder No.1312 Snake Eyes
yukicoder Advent Calendar Contest 2020 の 12 月 9 日公開問題です。
…この記事は、色変記事 Advent Calendar 2020 の12月9日公開の記事です。
色変記事アドベントカレンダー、なるものの募集を見ました。
色変記事AdventCalendarを作成しました。
— dokin (@ayoiyouyoeyo) November 4, 2020
みなさまの勇気ある宣言をお待ちしております!https://t.co/1NqMxq7Wu3
この恐ろしいアドベントカレンダーを見てしまった私。そういえば、AtCoder 青も Codeforces 紫も、近かったような……あれ、Topcoder も黄になれるんじゃ?
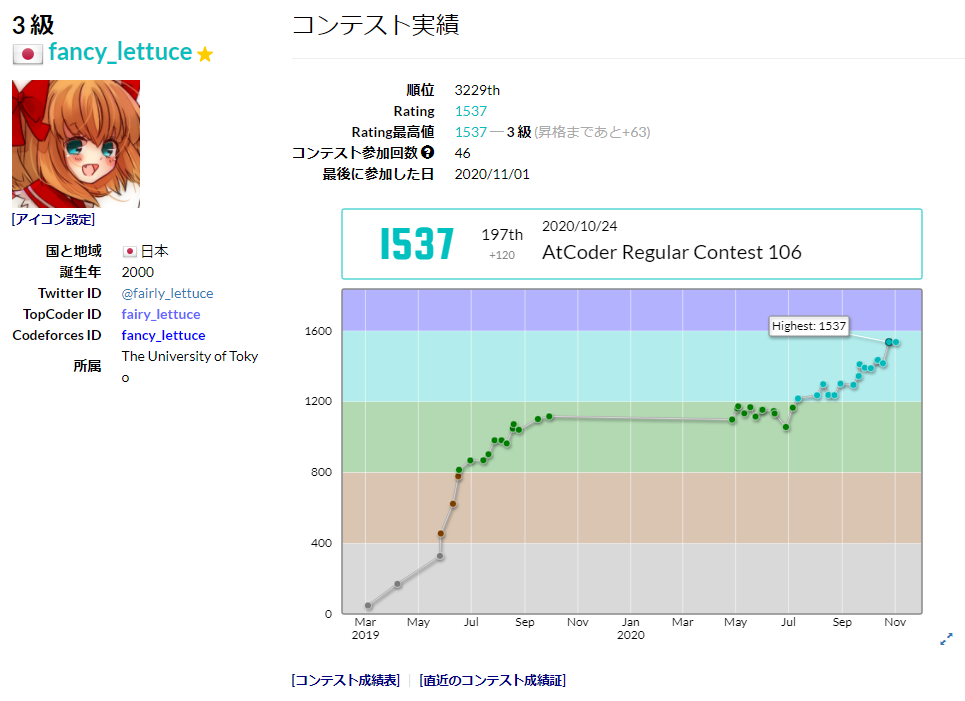
ということで、参加してみました。完全にノリですが、Topcoder はともかく AtCoder と Codeforces はずっと色変しないまま膠着していたので、これを期に色変してやろうと考えました。
(達成できたら)恐らく前代未聞の、3 コンテストサイト同時の色変記事になります。
…yukicoder Advent Calendar Contest 2020 の 12/08 出題問題です。
一見すると $N,\ S$ の間に簡単な法則が成り立ちそうですが、どうなんでしょう。面白いですね。
問題リンク
https://yukicoder.me/problems/no/1311
問題概要
ある順列が辞書順で出てくる順番をインデックスと呼びます。また、$S$ 要素で $1$-indexed な順列 $a$ に対して $b$ が $a_{b_{i}}=i (i=1,\ 2,\ \dots,\ s)$ を満たすとき、$b$ を $a$ の逆置換と呼びます。
$S$ 要素の順列の中で、$N$ 番目の順列の逆置換のインデックスを求めてください。
制約
$0\le N\lt S! \lt 2^{64}$
$1\le S\le 20$
yukicoder Advent Calendar Contest 2020 の 12/07 出題問題です。
みんながぐろふぉに出ている中の出題だったため1、FA を狙えないかと思っていましたが残念ながら 3 番目の AC でした。
問題リンク
https://yukicoder.me/problems/no/1310
問題概要
$N$ 要素の $+1,\ -1$ のどちらかからなる数列 $s$ に対して、
とします。ただし $s_{N+1}=s_{1}$ です。$2^{|E|}$ の総和を $998244353$ で割った余りを求めてください。
制約
$3\le N\le 2\times 10^{5}$
…数学問エスパーが成功したときほど気持ちいい瞬間はありません。
問題リンク
https://atcoder.jp/contests/arc110/tasks/arc110_d
問題概要
長さ $N$ の非負整数列 $A$ があります。長さ $N$、総和 $M$ 以下の非負整数列 $B$ 全てについて、$\displaystyle \prod_{i=1}^{N} \binom{B_i}{A_i}$ の総和を $10^9+7$ で割った余りを出力してください。
制約
$1\le N\le 2000$
$1\le M\le 10^9$
$1\le A_i \le 2000$
yukicoder Advent Calendar Contest 2020 の 12/03 出題問題です。
教育的問題除く ★4 初 AC!(★3.5 の AC が無いのは内緒) ちなみに 16 番目の AC でした。時間はかかったけれど、高難易度の問題をじっくり攻略するのは楽しいです。
おことわりですが、問題を解いた後ぼーっとしながら思考をそのまま書き連ねているので、解説の体を成していないかもしれません(ごめんなさい)。「考察」の内容は解説というよりは私の思考手順をなるべく細かく文章にしたものです。解説記事については、「私と同じ知識を有する人が同じ問題が全く分からなかった際に見て思考を追える文章」をモットーにしているので、いささか回りくどいかもしれません。その代わり、「解法」パートは簡潔に解き方をまとめようと思うので、どうかご容赦ください。
解説をどれくらいの細かさで書くかは本当に人々の思想だと思うんですけれど(ABC の解説を見ているとよく分かります……)、どうしたらいいんでしょうか……。
問題リンク
https://yukicoder.me/problems/no/1306
問題概要
インタラクティブ数当てゲーム。
$\{N,\ N+1,\ \dots ,\ N^2 -1\}$ をちょうど $1$ つずつ含む順列 $A$ があります。この順列を以下のクエリを高々 $1.5\times(N^2-N)$ 回行うことで特定してください。
? i j- $p=\lfloor A_i/N\rfloor-\lfloor A_j/N\rfloor$ とする。つまり、$A_i,\ A_j$ の $N$ の位の差。
- $q=\lfloor A_i%N\rfloor-\lfloor A_j%N\rfloor$ とする。つまり、$A_i,\ A_j$ の $1$ の位の差。
- もし $p\lt q$ なら $p,\ q$ を swap する。
- $p,\ q$ が返される。
数列を特定したら、! に続けて数列を出力してください。
ただし、出力したクエリによって完全に数列を特定できることができない状態で数列を答えても AC とはなりません(adaptive なジャッジ)。
制約
$2\le N\le 50$
…yukicoder Advent Calendar Contest 2020 の 12/02 出題問題です。
今気付いたんですが、これ yukicoder の記念すべき第 300 回目のコンテストらしいですね。
問題リンク
https://yukicoder.me/problems/no/1305
問題概要
太郎君を呼ぶためにあなたは以下のうちのどちらかの行動をします。
- 噂をする。$1$ 分後に太郎君は $1/p$ の確率で来る。そうでない確率 $(p-1)/p$ のときは再度どちらかの行動をする。
- 電話をして呼び出す。太郎君は $q$ 分後に必ず来る。
太郎君が来るまでの時間の期待値の最小値を求めてください。
制約
$1\le p,\ q\le 10^{9}$
入力は整数
大爆死。反省を込めて解説ブログを書きます。
問題リンク
https://codeforces.com/contest/1455/problem/D
問題概要
非負整数からなる数列 ${a_i}$ および非負整数 $x$ が与えられます。
$a_{i}>x$ である $a_{i},\ x$ を swap することを任意の回数できます。$a$ を広義単調増加にするためには最小で何回の操作を行えばいいでしょうか。
制約
$1\le t\le 500$ (テストケース数)
$1\le n\le 500$
$0\le x,\ a_i\le 500$
これ E よりも簡単じゃないですか?
問題リンク
https://codeforces.com/contest/1454/problem/F
問題概要
$n$ 要素からなる数列 $a$ があります。$a$ を $1$ 以上の要素からなる $3$ つの部分列に分けます。
最初の部分列の最大値、真ん中の部分列の最小値、最後の部分列の最大値が全て等しくなるような分け方は存在しますか。存在するときはその分け方も出力してください。
制約
$1\le t\le 2\times 10^{4}$ (テストケース数)
$3\le n\le 2\times 10^{5}$
$1\le a_{i} \le 10^{9}$
$\sum{n}\le 2\times 10^{5}$