yukicoder Advent Calendar Contest 2020 の 12/03 出題問題です。
教育的問題除く ★4 初 AC!(★3.5 の AC が無いのは内緒) ちなみに 16 番目の AC でした。時間はかかったけれど、高難易度の問題をじっくり攻略するのは楽しいです。
おことわりですが、問題を解いた後ぼーっとしながら思考をそのまま書き連ねているので、解説の体を成していないかもしれません(ごめんなさい)。「考察」の内容は解説というよりは私の思考手順をなるべく細かく文章にしたものです。解説記事については、「私と同じ知識を有する人が同じ問題が全く分からなかった際に見て思考を追える文章」をモットーにしているので、いささか回りくどいかもしれません。その代わり、「解法」パートは簡潔に解き方をまとめようと思うので、どうかご容赦ください。
解説をどれくらいの細かさで書くかは本当に人々の思想だと思うんですけれど(ABC の解説を見ているとよく分かります……)、どうしたらいいんでしょうか……。
問題リンク
https://yukicoder.me/problems/no/1306
問題概要
インタラクティブ数当てゲーム。
$\{N,\ N+1,\ \dots ,\ N^2 -1\}$ をちょうど $1$ つずつ含む順列 $A$ があります。この順列を以下のクエリを高々 $1.5\times(N^2-N)$ 回行うことで特定してください。
? i j- $p=\lfloor A_i/N\rfloor-\lfloor A_j/N\rfloor$ とする。つまり、$A_i,\ A_j$ の $N$ の位の差。
- $q=\lfloor A_i%N\rfloor-\lfloor A_j%N\rfloor$ とする。つまり、$A_i,\ A_j$ の $1$ の位の差。
- もし $p\lt q$ なら $p,\ q$ を swap する。
- $p,\ q$ が返される。
数列を特定したら、! に続けて数列を出力してください。
ただし、出力したクエリによって完全に数列を特定できることができない状態で数列を答えても AC とはなりません(adaptive なジャッジ)。
制約
$2\le N\le 50$
考察
$N$ の小さいときを考察します。$N=2$ とします。このとき、ありえる数列は $(2, 3),\ (3,\ 2)$ のどちらかです。ここでサンプル同様に ? 2 1 のクエリを出力すると、それぞれ 0 1 と -1 0 が帰ってきます。よって、$N=2$ のときはこれで十分特定できます。
$N=3$ のときです。ありえる数列は $\{3,\ 4,\ 5,\ 6,\ 7,\ 8\}$ の順列全てです。ここでは $(6,\ 5,\ 8,\ 7,\ 3,\ 4)$ を例に取ってみます。なお、$A_1=6=3\times 2+0$ であることに注意してください。
$2$ 個の数列の要素についての質問をできるタイプのインタラクティブ数列当てゲームの定石ですが、$1$ 個目を固定して他のものとの質問をします1。すると、クエリ ? 1 i $i=1,\ 2,\ 3,\ \dots$ の結果 $(p,\ q)$ はそれぞれ次のようになるはずです(便宜上 $i=1$ のクエリも含めていますが実際には質問しなくても問題ありません。また、以下では説明のため $(p, q)$ の順序はここでは変えずに下線を引くだけにしています)。
$(0,\ 0),\ (-1,\ 2),\ (0,\ 2),\ (0,\ 1),\ (-1,\ 0),\ (-1,\ 1)$
この結果から $A_1$ を復元できないか試みます。
$(p,\ q)$ の順序を変えていないため $N,\ 1$ の位の差が何回ずつ現れているかを見てみます。すると、$N$ の位の差には $-1,\ 0$ がそれぞれ $3$ 個、$1$ の位の差には $0,\ 1,\ 2$ がそれぞれ $2$ 個ずつ現れていると分かります。
両者で現れる値の範囲は $A_1$ の各位の値に依存していると考えられます。それでは、他の $A_1$ の値のときにそれぞれの範囲と現れる回数がどう動くかを確かめてみることにします。
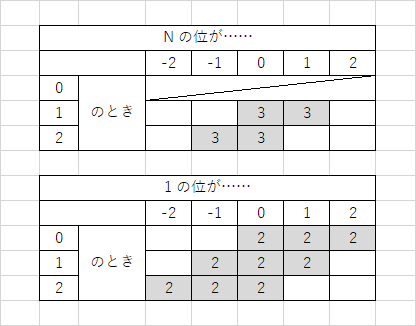
上のようになります。さらに一般の $N$ についても同様に考えると、
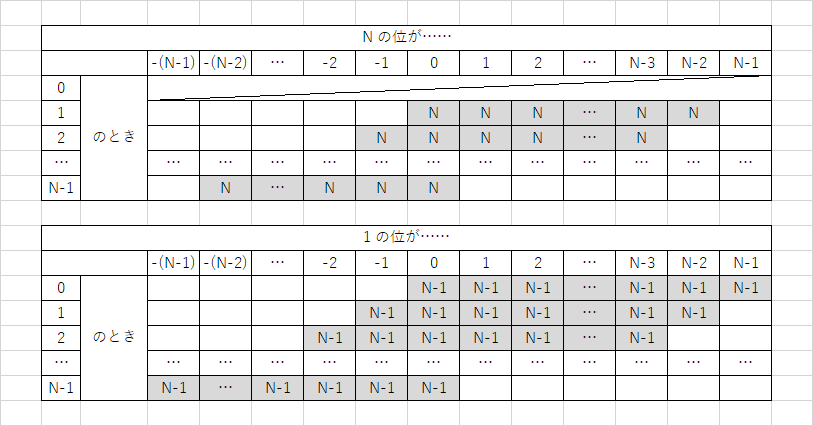
このようになります。
これより、それぞれの値の登場する回数は合計して $N-1,\ N,\ 2N-1$ のどれかであるため、それぞれの区間がどこにあるのかが分かります。これより $A_1$ は特定できます。
$A_1$ が特定できたらあとは得られた各 $(p,\ q)$ を手がかりに $A_i$ を復元することを考えます。
先程の例 $(6,\ 5,\ 8,\ 7,\ 3,\ 4)$ では $(p,\ q)$ の逆転した箇所は無いため、容易に復元できます。しかし、例えば $(3,\ 4,\ 5,\ 6,\ 7,\ 8)$ のような場合はどうなるでしょうか。
$(0,\ 0),\ (0,\ 1),\ (0,\ 2),\ \underline{(1,\ 0)},\ (1,\ 1),\ (1,\ 2)$
この場合は逆転したクエリが生まれています。そして、あろうことか逆転したあとの $(p,\ q)$ において $(0,\ 1)$ が $2$ つ存在しています。これでは区別ができないので、何か別のクエリで区別できないかを考えます。
$(p,\ q)$ は順序が区別できない状態で返されるため、$(p,\ q)$ が同じになってしまったふたつに関してクエリを質問することは無意味です。そこで、他の値と比較することで決定できないでしょうか。
ここで、$i,\ j$ に関しての $(p_i,\ q_i),\ (p_j,\ q_j)$ が同じ値になってしまう $i,\ j$ は、$(p_i,\ q_i)=(q_j,\ p_j)$ となる場合です。$N=3$ のときについて例示すると、そのような $i,\ j$ の組は下の図で太線となっているものの組の $1$ 通りです(下図では辺が $(p,\ q)$ の組に対応していることに注意してください)。

より一般的には、$p,\ q$ で現れる数の区間が被っている個数が $k$ 個であるとき、$k(k-1)/2$ 個の区別できない $(p,\ q)$ が存在します。$k$ は最大でも $N-1$ であるため、それぞれの区別できない箇所について $1$ 回ずつのクエリでどちらがどちらかを当てる作戦で行きましょう。
ところで、最初に見た例 $(6,\ 5,\ 8,\ 7,\ 3,\ 4)$ では $(p,\ q)$ の反転はありませんでした。そこで、先程の図 1 で $6$、つまり $A_1$ の $N$ の位が $2$、$1$ の位が $0$ のときを見てみると、それぞれの区間の重なりは $0$ のひとつのみです。このときは区別できない $(p,\ q)$ の組は $0$ です。
更に一般に、$A_1$ の $N,\ 1$ の位がそれぞれ $1, N-1$ または $N-1,\ 0$ であるとき、$A_1$ と他の数のクエリの答え $(p,\ q)$ は必ず区別できます。
ということで、そのどちらかを新しい基準にすれば両者を区別できるということになります。今回は私が通した際に使ったほうである $N,\ 1$ の位がそれぞれ $1,\ N-1$ であるときを考えます。
図 2 を眺めてもらえば分かると思いますが、$A_i$ の各位が $1,\ N-1$ のとき(それぞれ区間の左端と右端に対応します)は必ずしも区別できる領域にあるわけではありません(例: $A_1$ の各位が $N-1,\ N-1$ のとき)。そこで、$A_i$ が特定できなかった場合は、どのような $A_1$ であっても常に $(p,\ q)$ が区別できるもの、具体的には $A_i=N$ (各位は $1,\ 0$) を持ってきます(常に区別できることは容易に確かめられます)。
各位が $1,\ N-1$ である候補のどちらか片方について、それと各位が $1,\ 0$ である数のクエリで得られた $(p,\ q)$ は、それが予想通りの結果であればそれはその場所で合っていて、予想と違えば逆である、という判断材料になります。
これで判断基準となる軸の数が決定できました。あとは、軸の決定時と同じやり方で区別できないペアを全て決定していけば答えに辿り着けます。
解法
段階に分けて説明します。
$A_1$ と他を全部比較する (クエリ: $N(N-1)-1$ 回)
$A_1$ と $A_i\ (i=2,\ 3,\ \dots)$ を比較し、$(p,\ q)$ を保存しておきます。$(p,\ q)$ の逆引きを持っておくと嬉しいかもしれません。
$p,\ q$ 全て合計で現れた回数も記録しておき、そこから $A_1$ の $N,\ 1$ の位を復元できます(図 2 参照)。
$N$ である要素を探す (クエリ: $0$ 回)
$N$ である要素は $(p,\ q)$ がどちらも現れる中で最小であるペアである要素です。これより、$N$ の場所を特定します。
$N+(N-1)$ である要素を探す (クエリ: $0,\ 1$ 回)
もし一意に定まっている場合は次に進みます。
定まっていない、つまり $(p,\ q)$ がそれと同じものになる要素がもう一つある場合は、$A_1,\ N+(N-1)$ についてのクエリを投げたときに帰ってくると予想される $(p,\ q)$ と同じものがどちらであるかで $N+(N-1)$ が特定できます。
$(p,\ q)$ が区別できない組全てを特定する (クエリ: 最大 $(N-1)(N-2)/2$ 回)
特定した $N+(N-1)$ と区別できない要素 $A_i,\ A_j$ のどちらか(ここでは $A_i$ に投げるとする)についてクエリを投げます。それが $N+(N-1),\ A_i$ についてのクエリを投げたときに帰ってくると予想される $(p,\ q)$ と同じものがどちらかであるかで $A_i,\ A_j$ が特定できます。
以上で答えです。クエリの総数は $1.5\times N(N-1)/2$ を越えません。
実装
ちなみにですが、Ask() メソッドについて、私は ? i j が返すものを逆だと勘違いしていて、$N=2$ のケースすらも WA になってしまっていました。何故か本当に分からなくて、$N=2$ のみ通るサンプル通りのものを投げたらそのケースのみ AC したところで、ようやく気付きました。気付くまでは手元で色々なケースを試しデバッグしていたのでそこを直したら一発 AC。ちなみに AC までにかかった submit 数は驚きの 12 回。
絶対落ちるはずのないテストケースすら通らないときは根本的なミスが無いか確認しましょう。あと問題文を読みましょう。最近とても注意力が落ちています……。これが Rated じゃなくてよかった……。
今回は本当にぐちゃぐちゃコードです。ゴリ押ししました。
実装を展開する
public static void Solve(Scanner cin)
{
var n = cin.ReadInt();
var all = n * n - n;
//var a = cin.ReadIntArray(all);
int[] a = null;
var ans = SolveCheck(n, all, a, cin);
if (a != null)
{
for (int i = 0; i < all; i++)
{
if (a[i] != ans[i])
{
Console.WriteLine("Assertion Failed!");
Console.WriteLine($"n: {n}");
Console.WriteLine($"a: {a.Join(" ")}");
}
}
}
}
public static int[] SolveCheck(int n, int all, int[] a, Scanner cin)
{
int timesAsked = 0;
// if the return value is P, then ret[P + n] increments
var ret = new int[n * 2 + 1];
// the answers of the queries
var qa = new (int p, int q)[all];
var dic = new SortedDictionary<(int p, int q), List<int>>();
ret[n] += 2;
dic.Add((0, 0), new List<int>());
dic[(0, 0)].Add(0);
for (int i = 1; i < all; i++)
{
timesAsked++;
if (timesAsked > all * 3 / 2) throw new Exception();
var (p, q) = Ask(0, i, cin, a, n);
qa[i] = (p, q);
if (!dic.ContainsKey((p, q))) dic.Add((p, q), new List<int>());
dic[(p, q)].Add(i);
ret[p + n]++;
ret[q + n]++;
}
bool isBigDigit = false;
bool isSmallDigit = false;
int leftBigDigit = -1;
int rightBigDigit = -1;
int leftSmallDigit = -1;
int rightSmallDigit = -1;
for (int i = 0; i < n * 2 + 1; i++)
{
if (ret[i] == n || ret[i] == 2 * n - 1)
{
if (!isBigDigit) leftBigDigit = i - n;
isBigDigit = true;
}
else
{
if (isBigDigit) rightBigDigit = i - n;
isBigDigit = false;
}
if (ret[i] == n - 1 || ret[i] == 2 * n - 1)
{
if (!isSmallDigit) leftSmallDigit = i - n;
isSmallDigit = true;
}
else
{
if (isSmallDigit) rightSmallDigit = i - n;
isSmallDigit = false;
}
}
Debug.Assert(rightBigDigit - leftBigDigit == n - 1);
Debug.Assert(rightSmallDigit - leftSmallDigit == n);
var ans = new (int big, int small)[all];
ans[0] = (1 - leftBigDigit, -leftSmallDigit);
var oneZeroPair = (leftBigDigit, leftSmallDigit);
if (leftBigDigit > leftSmallDigit) oneZeroPair = (leftSmallDigit, leftBigDigit);
var oneZero = dic[oneZeroPair][0];
Debug.Assert(dic[oneZeroPair].Count == 1);
var zeroMaxPair = (big: leftBigDigit, small: rightSmallDigit - 1);
if (leftBigDigit > rightSmallDigit - 1) zeroMaxPair = (rightSmallDigit - 1, leftBigDigit);
var zeroMax = dic[zeroMaxPair][0];
if (dic[zeroMaxPair].Count >= 2)
{
var revMaxZeroPair = (zeroMaxPair.small, zeroMaxPair.big);
var genuine = (big: rightBigDigit - 1, small: leftSmallDigit);
var fake = (big: leftSmallDigit, small: rightBigDigit - 1);
var first = dic[zeroMaxPair][0];
var second = dic[zeroMaxPair][1];
var expected = (0, n - 1);
timesAsked++;
if (timesAsked > all * 3 / 2) throw new Exception();
var check = Ask(oneZero, first, cin, a, n);
if (expected == check)
{
zeroMax = first;
qa[first] = genuine;
qa[second] = fake;
}
else
{
zeroMax = second;
qa[first] = fake;
qa[second] = genuine;
}
}
foreach (var e in dic)
{
if (e.Value.Count >= 2)
{
var genuine = e.Key;
var fake = (p: e.Key.q, q: e.Key.p);
var expected = (big: ans[0].big + genuine.p - 1, small: ans[0].small + genuine.q - (n - 1));
if (expected.big > expected.small)
{
var t = expected.big;
expected.big = expected.small;
expected.small = t;
}
timesAsked++;
if (timesAsked > all * 3 / 2) throw new Exception();
var check = Ask(zeroMax, e.Value[0], cin, a, n);
if (expected == check)
{
qa[dic[e.Key][0]] = genuine;
qa[dic[e.Key][1]] = fake;
}
else
{
qa[dic[e.Key][0]] = fake;
qa[dic[e.Key][1]] = genuine;
}
}
}
for (int i = 0; i < all; i++)
{
var (p, q) = qa[i];
if (leftBigDigit <= p && p < rightBigDigit && leftSmallDigit <= q && q < rightSmallDigit)
{
// do nothing
}
else
{
var t = p;
p = q;
q = t;
}
ans[i] = (ans[0].big + p, ans[0].small + q);
}
var answer = ans.Select(p => p.big * n + p.small).ToArray();
Answer(answer);
return answer;
}
public static (int p, int q) Ask(int i, int j, Scanner cin, int[] ans, int n)
{
if (ans == null)
{
Console.WriteLine($"? {j + 1} {i + 1}");
Console.Out.Flush();
var (p, q) = cin.ReadValue<int, int>();
return (p, q);
}
else
{
Console.WriteLine($"? {j + 1} {i + 1}");
var p = ans[j] / n - ans[i] / n;
var q = ans[j] % n - ans[i] % n;
if (p > q)
{
var t = p;
p = q;
q = t;
}
Console.WriteLine($"\t{p} {q}");
Console.Out.Flush();
return (p, q);
}
}
public static void Answer(IEnumerable<int> a)
{
Console.WriteLine($"! {a.Join(" ")}");
Console.Out.Flush();
return;
}
ACコード: https://yukicoder.me/submissions/588549
感想
やっぱり数当てインタラクティブほど面白い競プロの問題はないです。この問題も考えているときは、なぜ通らないかウンウン悩みながらもずっと楽しかったです。Ad-hoc、最高!
それはそうと、日本語で上手く伝えるのって難しいです。考察パートは数学的に厳密な書き方を必ずしもせず感覚的な書き方を多くしていると思いますが、それが仇となり文章が読みにくくなることもあるので、うまい落とし所を見つけられるようになりたいです。
短時間で質の良く分かりやすい解説を書けるようになりたいですね。
この 1 ヶ月で解いたインタラクティブ数列当てゲーム、これで 3 問目なので、流石に一瞬で方針は立ちました。これが経験っていうものですね。たくさん問題を解くことの大切さを思い知りました。 ↩︎