灘中入試コンテストday2-E でした。実装が重かったです。無限に実装をバグらせてしまい、自らの実装力の無さを嘆きました。
問題リンク
https://yukicoder.me/problems/no/1354
問題概要
$x,\ y$ 座標ともに $0,\ 1,\ \dots,\ N$ からなる竹藪があります。サンボ君はこの竹藪の $M$ 個のチェックポイントを全て通りつつ $(0,\ 0)$ から $(N,\ N)$ へと移動したいです。移動は右または下にのみ可能です。
ただし、竹藪には $L$ 体のトラが棲んでいます。トラのいるマスには最大でも $K$ 回までしか通れません。
条件を満たすような移動のしかたは何通りあるでしょうか。$998244353$ で割った余りを求めてください。
制約
- $1\le N\le 2\times 10^{5}$
- $0\le M\le \min(10^5,\ N-1)$
- $0\le L\le \min(100,\ (N+1)^2-2)$
- $0\le K\le 10^5$
- チェックポイントの座標について、$0\lt xc_i,\ yc_i\lt N$
- $xc_i\lt xc_{i+1},\ yc_i\lt yc_{i+1}$
- トラの座標について、$0\le xt_i,\ yt_i\le N,\ (xt_i,\ yt_i)\ne (0,\ 0),\ (N,\ N)$
- トラの座標は Distinct
考察
まず、チェックポイントの座標は $x,\ y$ 座標ともに単調増加なので、チェックポイントごとに竹藪の盤面を区切ってそれぞれの結果をまとめる、という方針を取りたいです。区切った各区間について、トラを通る回数それぞれについての通り方の数を求めておけば、全体を通してトラを通る回数それぞれについての通り方の数は簡単な DP で求められます。
さて、それぞれの区間についての通り方の求め方です。細部は違いますが、この問題 (盤面の大きさがオーバーフローする可能性があるが、通れない場所の個数が少ない DP) は EDPC-Y - Grid 2 に非常に良く似た設定です。今回はトラを通る回数は $0$ 回だけでなく、それぞれの回数について求めなければならない点で EDPC-Y とは違う設定です。
では、EDPC-Y と似たような方針でトラのいる場所を順番に見ていきます。次のような盤面で考えてみましょう。S がチェックポイントの始点、G が終点、x がトラの位置です。また、以下の説明では $(x,\ y)$ という表記で $x,\ y$ 座標はそれぞれ縦軸・横軸を表すことに注意してください (例えば $(2,\ 1)$ はトラのいる位置です)。
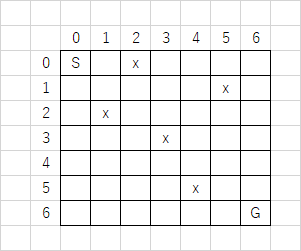
今回は貰う DP で考えます。$(3,\ 3)$ にいるトラについて、トラを通る回数がその時点で $p$ 回になるとします。
$p=2$ となるときは、それ以前にちょうど $1$ 回のみトラを通った場合です。これはこの前にいるトラのどちらかを通ってくる場合であり、簡単な二項係数の計算で場合の数は計算できます。
$p=1$ となるときは、どのトラも通らずにこのトラに辿り着く場合です。これは余事象を考えると、始点からこのトラに辿り着くための全ての通り方からこの前にいるトラのどちらかを通ってくる場合の数です。
次に、$(5,\ 4)$ にいるトラについて考えます。
$p=3$ となるときは、それ以前にちょうど $2$ 回トラを通った場合なので、$(3,\ 3),\ p=3$ の場合の数にそこから $(5,\ 4)$ へと移動してくる経路の数を掛けたものです。
$p=2$ となるときは、それ以前にちょうど $1$ 回トラを通った場合です。ここより前にいる $3$ 匹のトラの $p=1$ となる場合の数と、それぞれの位置から $(5,\ 4)$ に移動してくる経路の数を掛けたものの総和が場合の数になりそうです。しかし、これでは $(2,\ 1),\ (0,\ 2)$ から移動してくる時に $(3,\ 3)$ を通る場合を余計に数えています。このようになる場合の数は $p=3$ の場合の数でした。この場合の数を引けば良いです。
以上から分かりますが、そこに来るまでに一般に $p$ 回トラを通るような通り方の場合の数は、その前にいるトラに来るまでに $p-1$ 回トラを通る通り方の場合の数とそこからの経路の数の積を全て足し合わせた後、$p+1$ 回以上トラを通るような通り方を除けばよいです。
また、以上と同様にして終点まで辿り着く方法の数も数えることができます。
計算量ですが、トラの個体数は $L\le 100$ 匹であり、トラの全てのペアについて遷移するので DP の遷移自体は $O(L^2)$ 回行い、またトラを通った回数は $0,\ 1,\ 2,\ \dots,\ L$ 回の範囲を取るので、$O(L^3)$ で計算でき十分高速です。
解法
まず、各トラがどのチェックポイント間の区間に属するかで分類していきます。これは二分探索で可能です。また、チェックポイントを通る経路から外れた場所にいるトラのことは考慮しなくても良いので、この時点で除外しておきます。またトラの座標は $x$ 座標→ $y$ 座標の順などでソートしましょう。
それぞれの区間において $p$ 回トラを通るような通り方 $way_p$ を求めたいです。このために、$i$ 匹目のトラに辿り着く通り方で、$p$ 回トラを通るような通り方 $dp_{i,\ p}$ を定義し、これを求めます。
$dp_i$ の各値を求めるには $p$ が大きい順に計算すると良いです。$j$ を $j\lt i$ を満たすなかでトラ $i$ よりも $x,\ y$ 座標が小さいか等しいトラのインデックスとすると、
$\displaystyle dp_{i,\ p} = \sum_j dp_{j,\ p-1}\times \binom{x_j-x_i+y_j-y_i}{x_j-x_i} - \sum_{k=p+1}^{区間内のトラの数} dp_{i,\ k}$
というような遷移が成り立ちます。ただし、$dp_{i,\ 1}$ を計算するときのみ始点からトラ $i$ への経路を足すことを忘れないでください。
$dp$ の各値が計算できたら、終点へ辿り着く方法の数 $way_p$ を数えます。これも $dp$ の値と同様に次のように計算出来ます。ただし、$a,\ b$ は区間の始点から終点の $x,\ y$ への移動する座標です。
$\displaystyle way_{p} = \sum_i dp_{i,\ p}\times \binom{a-x_i+b-y_i}{a-x_i} - \sum_{k=p+1}^{区間内のトラの数} way_{p}$
$way_0$ の計算のときに始点から終点への経路数を足すことを忘れないでください。
各区間の場合の数が計算できたら、それまでの区間でトラを $s$ 回通るような通り方の数を $prev_s$、今見ている区間まででトラを $s+p$ 回通るような通り方の数を $ans_{s+p}$とすると、
$ans_{s+p}$ += $prev_s\times way_{p}$
という DP によって更新できます。
実装
実装を展開する
bool isMultipleTestCases = false;
ModInt[] factorial, finv;
public void Solve()
{
Init();
var (n, m, l, k) = sr.ReadValue<int, int, int, int>();
var checkpoint = new List<(int x, int y)>();
var checkx = new List<int>();
checkpoint.Add((0, 0));
checkx.Add(0);
for (int i = 0; i < m; i++)
{
var xy = sr.ReadValue<int, int>();
checkpoint.Add(xy);
checkx.Add(xy.Item1);
}
checkpoint.Add((n, n));
checkx.Add(n);
var square = new List<(int x, int y)>();
for (int i = 0; i < checkpoint.Count - 1; i++)
{
square.Add((checkpoint[i + 1].x - checkpoint[i].x, checkpoint[i + 1].y - checkpoint[i].y));
}
var tiger = Enumerable.Repeat(0, m + 1).Select(p => new List<(int x, int y)>()).ToArray();
for (int i = 0; i < l; i++)
{
var (x, y) = sr.ReadValue<int, int>();
var ok = -1;
var ng = m + 1;
while (ng - ok > 1)
{
var mid = ok + (ng - ok) / 2;
if (x >= checkpoint[mid].x && y >= checkpoint[mid].y) ok = mid;
else ng = mid;
}
var index = ok;
if (x < checkpoint[index].x || x > checkpoint[index + 1].x) continue;
if (y < checkpoint[index].y || y > checkpoint[index + 1].y) continue;
tiger[index].Add((x - checkpoint[index].x, y - checkpoint[index].y));
}
for (int i = 0; i < m + 1; i++)
{
tiger[i].Sort();
}
var ans = new ModInt[l + 1];
ans[0] = 1;
for (int i = 0; i < m + 1; i++)
{
ModInt t = 0;
var exclude = Enumerable.Repeat(0, tiger[i].Count).Select(p => new ModInt[tiger[i].Count + 1]).ToArray();
for (int j = 0; j < tiger[i].Count; j++)
{
var all = Binom(tiger[i][j].x + tiger[i][j].y, tiger[i][j].x);
ModInt sum = 0;
for (int p = tiger[i].Count; p >= 1; p--)
{
if (p == 1) exclude[j][p] += all;
for (int s = 0; s < j; s++)
{
var x = tiger[i][j].x - tiger[i][s].x;
var y = tiger[i][j].y - tiger[i][s].y;
if (x < 0 || y < 0) continue;
exclude[j][p] += exclude[s][p - 1] * Binom(x + y, x);
}
exclude[j][p] -= sum;
sum += exclude[j][p];
}
}
{
var all = Binom(square[i].x + square[i].y, square[i].x);
var way = new ModInt[tiger[i].Count + 1];
ModInt sum = 0;
for (int p = tiger[i].Count; p >= 0; p--)
{
if (p == 0) way[p] += all;
for (int s = 0; s < tiger[i].Count; s++)
{
var x = square[i].x - tiger[i][s].x;
var y = square[i].y - tiger[i][s].y;
way[p] += exclude[s][p] * Binom(x + y, x);
}
way[p] -= sum;
sum += way[p];
}
var next = new ModInt[l + 1];
for (int s = l; s >= 0; s--)
{
for (int u = tiger[i].Count; u >= 0; u--)
{
if (s + u > l) continue;
next[s + u] += ans[s] * way[u];
}
}
ans = next;
}
}
ModInt ansall = 0;
for (int i = 0; i <= Min(k, l); i++)
{
ansall += ans[i];
}
Console.WriteLine(ansall);
}
public ModInt Binom(int n, int r) => factorial[n] * finv[r] * finv[n - r];
public void Init()
{
factorial = new ModInt[400005];
finv = new ModInt[400005];
factorial[0] = 1;
finv[0] = 1;
for (int i = 1; i < 400005; i++)
{
factorial[i] = factorial[i - 1] * i;
finv[i] = factorial[i].Inverse();
}
}
ACコード: https://yukicoder.me/submissions/607346
感想・反省
約 110 行の重実装問題でした。デバッグがとにかくつらかった……。2 時間ありましたが結局コンテスト中には通せず、自分の実装力の無さを痛感しました。
コンテスト中は主に DP パートのデバッグに苦戦しましたが、サンプル 3 がどうしても合わずうんうんと唸っていました。何が違うのかも分からず、コンテスト後にじっくり見てみるとなんとチェックポイントの振り分けがきちんと出来ていないことに気付きました。トラを振り分ける部分を頑張って書こうとしましたが二分探索をバグらせまくってしまい、とても悲しくなりました。
実装力は非常に難解なコードを書き上げる能力というより1、簡単なコードを混乱せずにすぐ、正確に書き上げる能力だと痛感しました。これはまさに ABC で求められる早解き能力ですね。この問題はそこそこ難しい (黄 diff 相当だと感じました) と思いますが、難しい問題でそのような実装で詰まると悲しい思いをしますね。ABC 早解きはそこそこ得意な方ですが、たまにこういうハマり方をする (というよりは、高難易度耐性がないので高難易度の部分問題をバグらせがち、なのかも) のでたくさん重実装問題を解いて慣れたい次第です。
問題そのものはとても面白かったです。特に高難易度数学問量産の PCT みたいなイメージがあるので、このような典型の難しめの応用の DP 問題が書けるんだとちょっとびっくりしました。氏が書くこういう問題ももっと見てみたいです。
それが必要なこともあると思いますが。 ↩︎