yukicoder contest 275 より。
個人差が強い問題。発想出来るかが分かれ目？yukicoder problems では黄 diff とのことですが¹、人によっては黄相応だと思う人も青程度と思う人もいると思います。

問題リンク

https://yukicoder.me/problems/no/1293

問題概要

$N$ 個の都市には $D$ 本の自動車専用道路と $W$ 本の歩行者専用があります。
$0$ 本以上の自動車専用道路を通った後に $0$ 本以上の歩行者専用道路を通ることで移動できる都市のペアの個数(自身どうしのペアを含まない)を求めてください。

制約

$2\le N\le 10^{5}$
$1\le D,\ W\le \min\left(10^{5},\ \frac{N(N-1)}{2}\right)$

考察

連結成分を考えればいいことはすぐ分かるので、とりあえず Union-Find 木を使う方針で考えます。自動車専用道路と歩行者専用道路の連結成分は簡単に分かりますが、順に通ると移動できるという条件はどうすればいいのかが肝になってきます。

ここでは、下図のような場合を例として思考の手順を説明します。

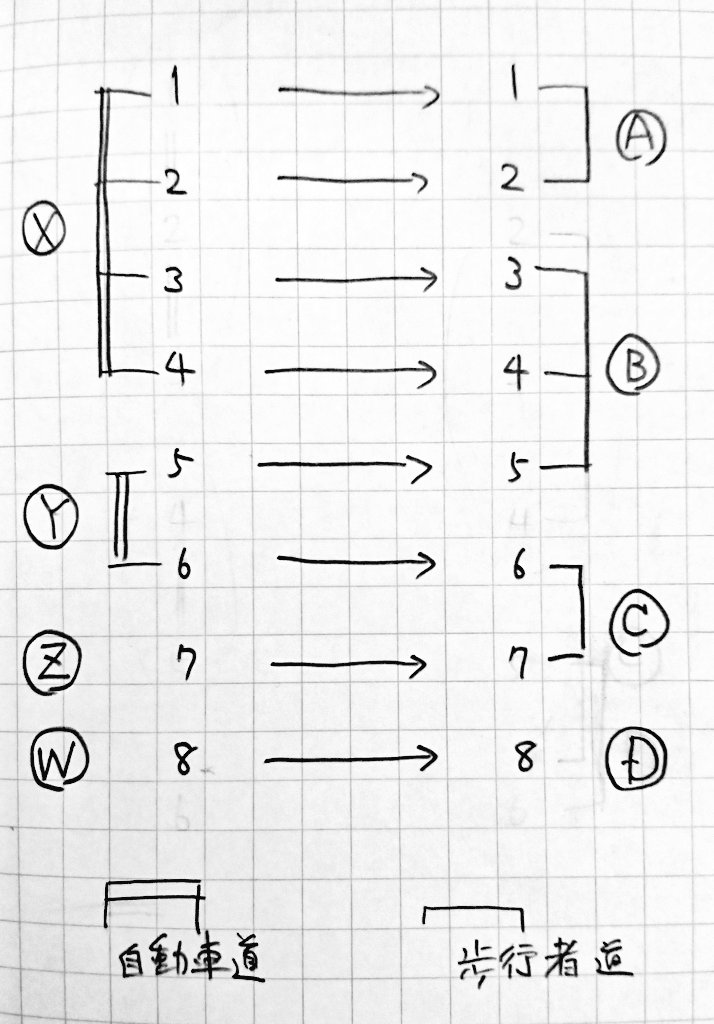
自動車専用道路の連結成分を上から順に $X,\ Y,\ Z,\ W$、歩行者専用道路の連結成分を上から順に $A,\ B,\ C,\ D$ と名付けます。

$X,\ Y,\ Z,\ W$ それぞれに属する頂点からどの頂点まで移動できるかを見ていきます。以降、自動車専用道路と歩行者専用道路を切り替える都市を切り替え都市と呼ぶことにします。

• $X$ 内のどの頂点から出発しても、頂点 $1,\ 2$ のどちらかを切り替え都市にすると $A$ の各都市、$3,\ 4$のどちらかを切り替え都市にすると $B$ の各都市に移動でき、計 $5$ 都市に移動できます。

• $Y$ 内のどの頂点から出発しても、頂点 $5$ を切り替え都市にすると $B$ の各都市、$6$を切り替え都市にすると $C$ の各都市に移動でき、計 $5$ 都市に移動できます。

• $Z$ 内の頂点 $7$ を切り替え都市にすると $C$ の計 $2$ 都市に移動できます。

• $W$内の頂点 $8$ を切り替え都市にすると $D$ の $1$ 都市にのみ移動できます。

以上で見たことを踏まえると、次のようなことが考察できます。

• 自動車から歩行者へ切り替えるまでに自動車専用道路なら自由に通れるため、自動車専用道路の連結成分内の各頂点から移動できる頂点は全て同じ頂点の集合になる。
• 自動車専用道路の連結成分内の各頂点を切り替え都市としたときに、その切り替え都市が属する歩行者専用道路の連結成分の頂点に行くことができる。

ここで、自動車と歩行者の各連結成分を二部グラフのように見立て、切り替え都市が自動車の連結成分と歩行者の連結成分を繋ぐ辺である、と考えると下図のように見ることができます。

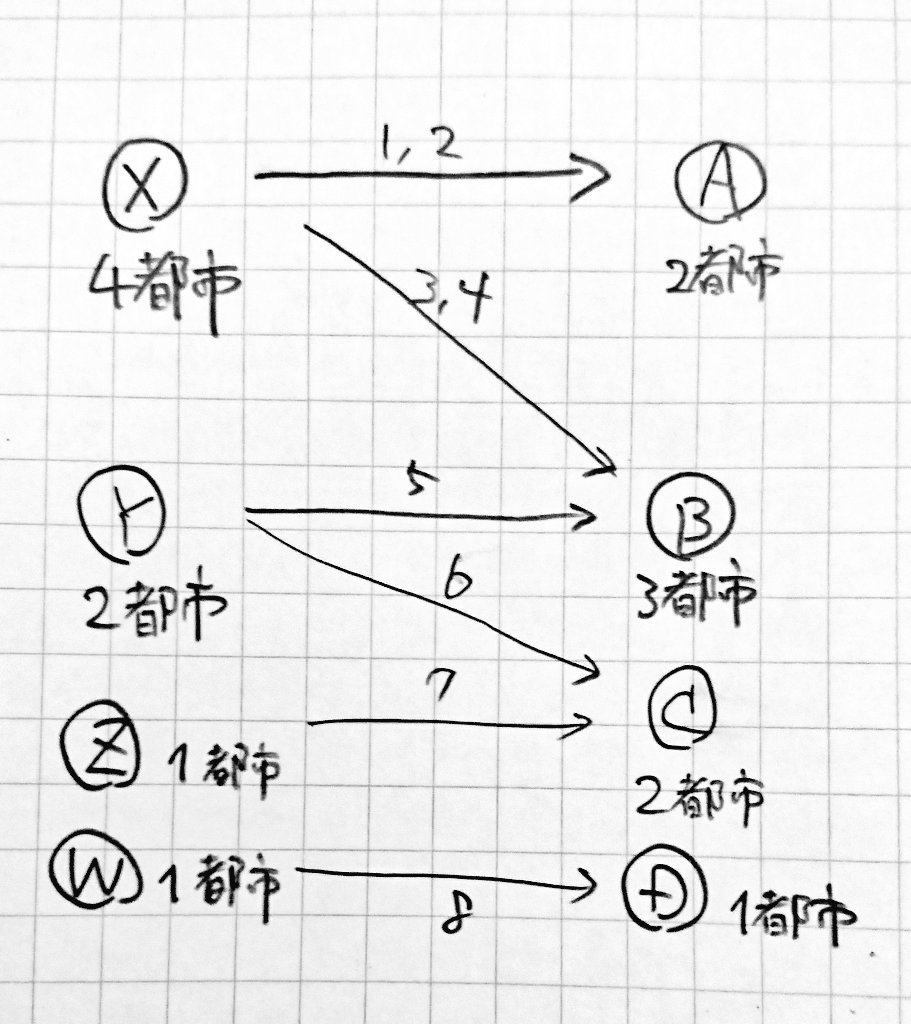
これからも分かるように、$4\times (2+3)+2\times (3+2)+1\times 2+1\times 1=33$ 通りの移動できる頂点のペアが存在します。但し、ある頂点から同じ頂点に行く場合も含まれているので、答えは頂点数 $8$ を引いて $25$ と分かりました。

より一般には、自動車専用道路の各連結成分($X,\ Y,\ Z,\ W$)から行ける歩行者専用道路の連結成分($A,\ B,\ C,\ D$)を重複がないよう管理して、移動の仕方をそれぞれ計算し足し合わせればよいことが分かります。

解法

基本的に考察で述べたとおりです。自動車専用道路の連結成分と歩行者専用道路の連結成分を Union-Find 木で求め、各連結成分のサイズを事前に求めておきます。
自動車・歩行者それぞれの連結成分を結ぶパートについては、ふたつの Union-Find 木の親どうしを結べばよいです。具体的には、頂点 $i$ を親とする(自動車の)連結成分から行くことができる(歩行者の)連結成分の親頂点を管理する set[i] を用意します²。 最後に、自動車の連結成分の親となっている頂点それぞれについて、(その自動車専用道路の連結成分のサイズ)と(その自動車専用道路の連結成分から行くことが出来る歩行者専用道路の連結成分の頂点数の総和)の積を求め、それらの総和を計算すればよいです。最後に $N$ を引くことを忘れないでください。

計算量についてですが、切り替え都市の個数(二部グラフとしたときの辺)は高々 $N$ 個であるため、連結成分単位で移動の仕方を考えた場合は十分高速であると考えられます。

実装

私の AC コードを載せます。C# ですが、以上の解説を読めばだいたい意味は伝わると思います。
なお、automobile は自動車、pedestrian は歩行者の専用道路の連結成分を求める Union-Find の変数名です。

public static void Solve(Scanner cin)
{
	var (n, _d, _w) = cin.ReadValue<int, int, int>();
	var (a, b) = cin.ReadValueArray<int, int>(_d);
	var (c, d) = cin.ReadValueArray<int, int>(_w);

	var automobile = new UnionFind(n);
	var pedestrian = new UnionFind(n);
	for (int i = 0; i < _d; i++)
	{
		automobile.Unite(a[i] - 1, b[i] - 1);
	}
	for (int i = 0; i < _w; i++)
	{
		pedestrian.Unite(c[i] - 1, d[i] - 1);
	}
	for (int i = 0; i < n; i++)
	{
		automobile.Find(i);
		pedestrian.Find(i);
	}

	var autoSize = new long[n];
	var pedeSize = new long[n];
	for (int i = 0; i < n; i++)
	{
		autoSize[automobile.Find(i)]++;
		pedeSize[pedestrian.Find(i)]++;
	}

	var autoToPede = new Set<int>[n];
	for (int i = 0; i < n; i++)
	{
		autoToPede[i] = new Set<int>();
	}
	for (int i = 0; i < n; i++)
	{
		autoToPede[automobile.Find(i)].Add(pedestrian.Find(i));
	}
	long ans = 0;
	for (int i = 0; i < n; i++)
	{
		if (autoSize[i] == 0) continue;
		var sum = 0L;
		foreach (var e in autoToPede[i])
		{
			sum += pedeSize[e];
		}
		sum *= autoSize[i];
		ans += sum;
	}
	ans -= n;
	Console.WriteLine(ans);
}

ACコード: https://yukicoder.me/submissions/581825

感想

自動車専用道路の連結成分と歩行者専用道路の連結成分を二部グラフに見立てるのは個人的にも話がまとまりやすくなると思います。これもとても良い問題だと思います。作問者の沙耶花さんを素直に尊敬します。

あと解説が漢字が多くてごちゃごちゃしてますね、後でもう少し読みやすくするために校正を加えるかもしれません(この解説は速報のようなものということで、お許し下さい……)。