yukicoder contest 275 より。
実装ゲーでした。

問題リンク

https://yukicoder.me/problems/no/1292

問題概要

辺 a, b, c からなる面積 $1$ の三角形があります。どの辺について対称移動させるかの順序が文字列 $S$ で与えられるので、通過する面積を求めてください。

制約

$1\le |S| \le 2\times 10^{5}$

考察・解法

頂点を持つのは面倒そうだから、位置と辺を考えることにしようと思います。まず、図を書いて各辺がどういう位置関係になるかを考察してみます。

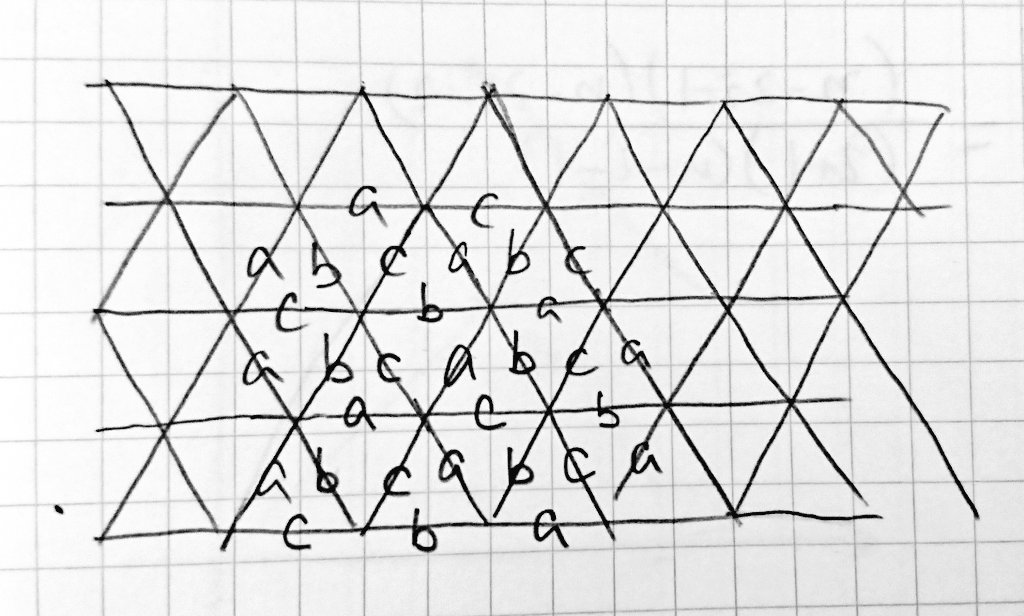
これを見ながら実装を考えることにします。じっとよく見ると、上向きと下向きの三角形ではそれぞれ表裏が決まっている(すなわち、回転と平行移動のみで各辺を一致させられる)ことが分かります。そこで、水平($x$ 軸に平行)な辺のみを考えればどの向きに対称移動すればいいか分かるようになります。以下、水平な辺のことを「底辺」と呼びます。

対称移動を実装できれば、あとは三角形が存在した位置の個数を出力すればよいです。これは set などで容易に実現できます。

実装

私の実装における場合分けは、

• 上向きか下向きか
• 底辺と対称移動する軸の辺の位置関係

の計 $6$ 通りです。また、底辺はa / b / cをそれぞれ $0,\ 1,\ 2$ として管理し、三角形の位置を $x,\ y$ 座標で管理しています(下図参照)。

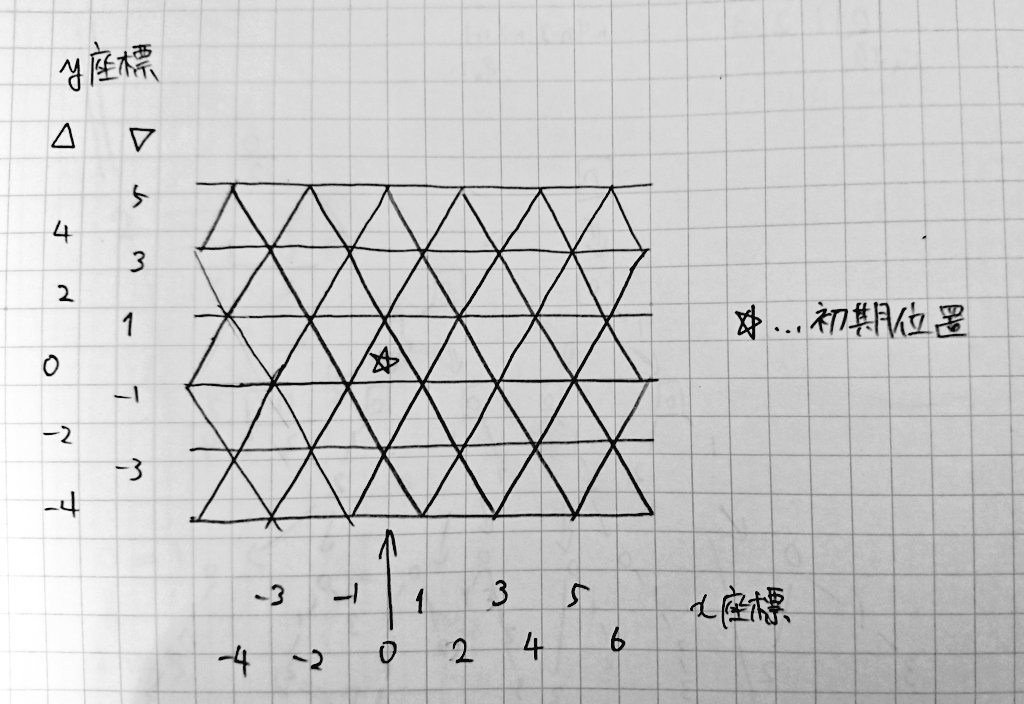
座標は上向きと下向きで互い違いに偶数・奇数になっています(すると座標の変化の実装が非常に楽です)。

場合分けについては、底辺と軸の辺が同じ場合は、底辺をそのまま上向きと下向きを反転させます。$y$ 座標もそれに応じて変化させます。
そうでない場合は、位置関係に注意しつつ底辺を $+1$ ないし $-1$ し、$x,\ y$ 座標を変化させます。底辺の値を変えるときは全て $\mathbb{Z}_{3}$ で考えるものとします¹。

public static void Solve(Scanner cin)
{
	var s = cin.ReadString();
	bool isRev = false;
	int x = 0;
	int y = 0;
	var root = 0;
	var seen = new SortedSet<(int x, int y)>();
	seen.Add((0, 0));
	for (int i = 0; i < s.Length; i++)
	{
		if (isRev)
		{
			if (root == s[i] - 'a')
			{
				y++;
			}
			else if ((root + 1) % 3 == s[i] - 'a')
			{
				x--;
				y--;
				root = (root + 2) % 3;
			}
			else
			{
				x++;
				y--;
				root = (root + 1) % 3;
			}
			isRev = false;
		}
		else
		{
			if (root == s[i] - 'a')
			{
				y--;
			}
			else if ((root + 1) % 3 == s[i] - 'a')
			{
				x--;
				y++;
				root = (root + 2) % 3;
			}
			else
			{
				x++;
				y++;
				root = (root + 1) % 3;
			}
			isRev = true;
		}
		seen.Add((x, y));
	}
	Console.WriteLine(seen.Count);
}

ACコード: https://yukicoder.me/submissions/581721

感想

面白い問題でした。実装を簡略化するためにはどうすればいいかを学べる良問だと思います。