C 問題は問題文が読みにくくて少しつらかったけど、D 問題も E 問題も面白くて楽しいセットでした。本番ギリギリ E が間に合わなくてつらかった……。
問題リンク
https://codeforces.com/contest/1469/problem/E
問題概要
ふたつの文字列 $a,\ b$ について、同じ位置に同じ文字が存在するような位置がひとつでもある場合、a bit similar といいます。
0 および 1 からなる文字列 $s$ について、その長さ $k$ の部分文字列全てと a bit similar である長さ $k$ の文字列のうち、辞書順最小のものを求めてください。そのような文字列が存在しない場合はその旨を報告してください。
制約
$1\le k\le n\le 10^6$
考察・解法
サンプルケースでそれぞれの部分文字列を書き出してみます。ここではサンプルケースのうち 3 つ目について考えてみます。

このような感じです。さて、0 1 からなる文字列のうち長さ $k=3$ のものを列挙し、今回のケースでは現れないものを黒塗りするとこのようになります。
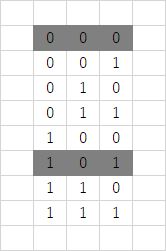
では、今回のケースで現れない部分文字列について、その各桁を反転させたもの (例えば 010 ならば 101) を考えると、全ての部分文字列とその文字列は a bit similar であることが示せます。逆に、現れる部分文字列の各桁を反転させたものは、その部分文字列そのものと必ず a bit similar ではないため、条件を満たしません。
これより、長さ $k$ の文字列全てが登場する場合はそのような文字列は存在せず、登場しない文字列が存在する場合はそのような文字列のうち辞書順最大のものを反転させたものが答えとなります。今回の場合は 101 を反転させた 010 が答えです。
ですが、この解法を愚直に実装すると、部分文字列の列挙で $O(nk)$、長さ $k$ の文字列の列挙で $O(2^k)$ の空間または時間計算量がかかってしまいます。そこで、上手い具合に不必要な情報を落とせないか見てみます。
文字列 $s$ の部分文字列は全部で $n-k+1$ 通りあり、長さ $k$ の文字列は全部で $2^k$ 通り存在します。よって、長さ $k$ の文字列を全部確認することは冗長です。答えたいのは現れない部分文字列のうち辞書順最大のものでしたので、ここでは x を 0 と 1 どちらでもよいものとして、111...1xx...xx の形で表される文字列を考えます。ここでは x の桁数を $p$ 桁とします。
このように表される文字列は $2^p$ 個存在しますが、$n-k+1$ 個を越える $p$ について、必ずそのような文字列の中で部分文字列として現れない文字列が存在します。ここで、$p$ の最小値は $O(\log({n-k+1}))=O(\log{n})$ であることに注意してください。
よって、1 の続く桁数が $k-p$ 未満となる場所を枝刈りした後、x となる桁のみを考慮すればよいことが分かります。$p$ は $O(\log{n})$ であり高々 $20$ であることを考えると、全体の計算量は $O(n\log n)$ となり、間に合います。
実装
文字列のうち 1 が何個連続で現れるかは累積和のような感じのものを作っておけば前準備 $O(n)$・クエリ $O(1)$ で答えられます。
文字列のうち現れないものを set などで管理しようとすると余計な $\log$ が付いてしまうので TLE しかねません (私は本番で TLE しました)。なので、$2^p$ 個からなる配列を用意するなどして $\log$ のつかないような実装をする必要があります。
実装を展開する
public void Solve()
{
var (n, k) = cin.ReadValue<int, int>();
var s = cin.ReadString();
int p = 1;
while (p <= k && (1 << p) <= n - k + 1)
{
p++;
}
p.Chmin(k);
var rep1 = new int[n + 1];
for (var i = n - 1; i >= 0; i--)
{
if (s[i] == '1') rep1[i] = rep1[i + 1] + 1;
else rep1[i] = 0;
}
var app = new bool[1 << p];
var baseStr = Enumerable.Repeat('1', k - p).Join();
for (var i = 0; i < n - k + 1; i++)
{
if (rep1[i] >= k - p) app[Convert.ToInt32(s.Substring(i + k - p, p), 2)] = true;
}
for (var i = app.Length - 1; i >= 0; i--)
{
if (!app[i])
{
YESNO(true);
var ans = (baseStr + Convert.ToString(i, 2).PadLeft(p, '0')).ToCharArray();
for (var j = 0; j < ans.Length; j++)
{
ans[j] = ans[j] == '0' ? '1' : '0';
}
Console.WriteLine(ans.Join());
return;
}
}
YESNO(false);
}
ACコード: https://codeforces.com/contest/1469/submission/102626759
感想
鳩の巣原理で解ける問題はとてもエレガントで好きです!
おひるねしてたら寝過ごしてしまい、序盤 10 分を棒に振ってしまったことを非常に後悔しています。10 分あったらこの問題通せていた……。