Div. 3 全完しようと思ったらこの問題に阻まれてしまいました。どう考えても不可能だと思ってたけど、よくよく見たらなもりグラフという制約を見逃していました。恥ずかしい。
問題リンク
https://codeforces.com/contest/1454/problem/E
問題概要
自己ループや多重辺のない $n$ 頂点 $n$ 辺の連結グラフ(つまり、なもりグラフ1)が与えられます。このグラフに含まれる長さが $1$ 以上の単純パスの数を求めてください。ただし、逆順にたどっただけのパスは同じものとみなします。
制約
$1\le t\le 2\times 10^{4}$ (テストケース数)
$3\le n\le 2\times 10^{5}$
$\sum{n}\le 2\times 10^{5}$
考察・解法
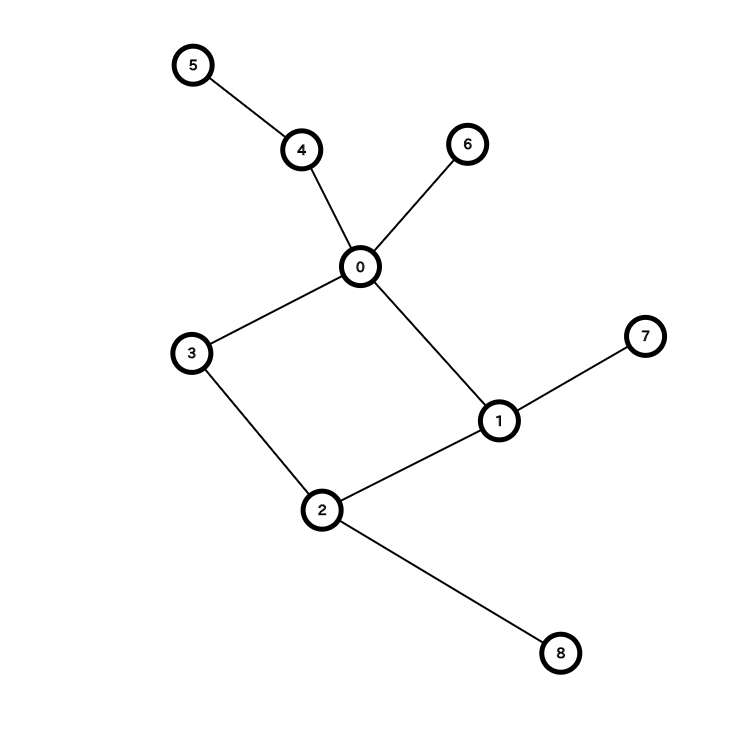
こういうグラフで考察してみます。2
なもりグラフは木に $1$ 辺が追加されたもの、ということでした。木のパスはふたつの頂点が指定されたら一意に定まるため、木の単純パス数は全ての頂点間のペアの数と同じです。では、なもりグラフでのパスではどうなるのか考えてみます。
木ではパスは一意に定まるので、ループが関係ない頂点間(たとえば、頂点 $0,\ 6$ や $2,\ 8$ など)のパスは $1$ 通りです。
ループが関係する場所では、たとえば頂点 $0,\ 1$ 間のパスは $0,\ 1$ と $0,\ 3,\ 2,\ 1$ の $2$ 通り存在します。頂点 $5,\ 8$ 間のパスは $5,\ 4,\ 0,\ 1,\ 2,\ 8$ と $5,\ 4,\ 0,\ 1,\ 3,\ 8$ の $2$ 通り存在します。これらはどちらも、ループのどちら側を通るかによって $2$ 通りに分かれています。
以上から、ループに含まれる辺を通らないといけない頂点間のパスは $2$ 通り、そうでない頂点間は $1$ 通りと分かります。
ループに含まれる辺を消した連結成分を考えます。下図のようになります。
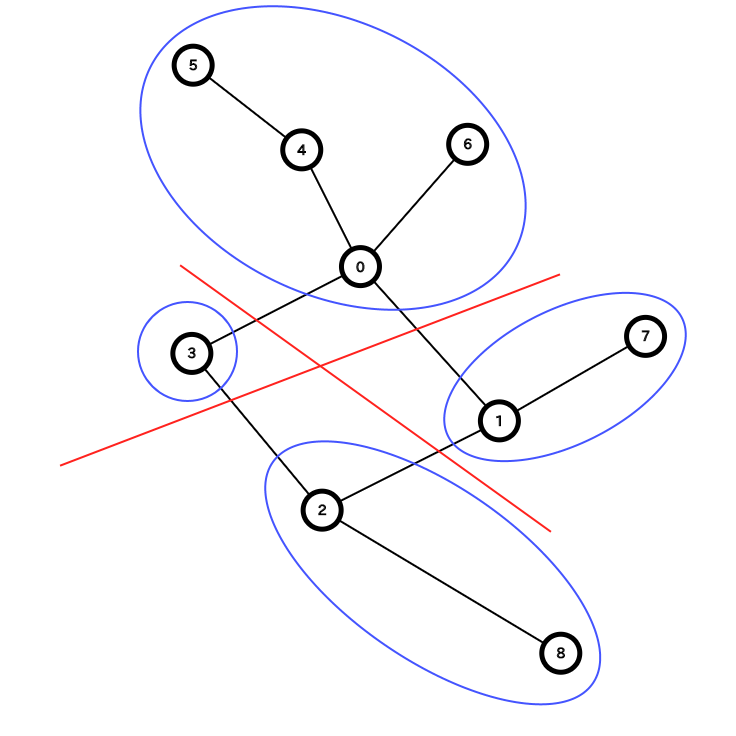
これを見ると、ループ外の辺のみを伝っていけるのはこの連結成分(青丸)の中の頂点間で、それ以外は全てループに含まれる辺を通らないといけない頂点対と分かります。よって、全頂点のペア数 $N(N-1)/2$ から各連結成分の頂点のペア数 (連結成分の頂点数を $v$ として、$v(v-1)/2$ 個) を引いていったものが答えです。連結成分は $O(N)$ 個であるため、十分間に合います。
実装
なもりグラフのループ検出は、DFS によって可能です。けんちょんさんの Qiita が詳しいです。
ループ外の連結成分は Union-Find や DFS/BFS によって可能です。グラフの辺のうちどちらの頂点もループに含まれない頂点のみ連結していく、と考えると Union-Find のほうが楽だと思います。
実装を展開する
public static void Solve(Scanner cin)
{
int _t = cin.ReadInt();
for (int _i = 0; _i < _t; _i++)
{
var n = cin.ReadInt();
var (u, v) = cin.ReadValueArray<int, int>(n);
var g = new List<List<int>>();
for (int i = 0; i < n; i++)
{
g.Add(new List<int>());
}
for (int i = 0; i < n; i++)
{
g[u[i] - 1].Add(v[i] - 1);
g[v[i] - 1].Add(u[i] - 1);
}
var seen = new bool[n];
var finished = new bool[n];
var loopnum = -1;
var q = new Queue<int>();
var history = new Stack<int>();
bool ok = false;
var ret = DFS(g, 0, -1, history, seen, finished);
var loop = new bool[n];
while (history.Count > 0)
{
var cur = history.Pop();
loop[cur] = true;
if (cur == ret) break;
}
var uf = new UnionFind(n);
for (int i = 0; i < n; i++)
{
if (loop[u[i] - 1] && loop[v[i] - 1]) continue;
uf.Unite(u[i] - 1, v[i] - 1);
}
for (int i = 0; i < n; i++)
{
uf.Find(i);
}
var sd = new SortedDictionary<int, int>();
for (int i = 0; i < n; i++)
{
var p = uf.Find(i);
if (!sd.ContainsKey(p)) sd.Add(p, 0);
sd[p]++;
}
long ans = (long)n * (n - 1);
foreach (var e in sd)
{
ans -= (long)e.Value * (e.Value - 1) / 2;
}
Console.WriteLine(ans);
}
}
public static int DFS(List<List<int>> g, int v, int prev, Stack<int> history, bool[] seen, bool[] finished)
{
var ret = -1;
seen[v] = true;
history.Push(v);
foreach (var e in g[v])
{
if (e == prev) continue;
if (finished[e]) continue;
if (seen[e] && !finished[e]) return e;
ret = DFS(g, e, v, history, seen, finished);
if (ret != -1) return ret;
}
history.Pop();
finished[v] = true;
return ret;
}
ACコード: https://codeforces.com/contest/1454/submission/99502081
感想
なもりグラフじゃないと思ってたときはパスの長さが関係あるのかなと思っていましたが、全く違いました。
焦らずに問題文をちゃんと読む癖を付けたいです。
ループをただ $1$ つのみ持ち、そのループの周りにひげが生えたような形のグラフ。木に $1$ 辺を足したグラフともみることができます。名前の由来は『ゆるゆり』作者であるなもり先生の Twitter アイコン。 ↩︎
このグラフの画像は CS Academy の Graph Editor で生成しました。今回はあまり調整していないので形が整っていませんが(ごめんなさい……)、非常に優秀なツールです。 ↩︎