同じ日の ARC で -55 もレート溶かしたのに同じ日のこどふぉでレート超盛りました。Codeforces は調子いいのに、AtCoder の下振れが酷いです。助けて。
問題リンク
https://codeforces.com/contest/1451/problem/D
問題概要
$x-y$ 座標上の円 $x^{2}+y^{2}=d^{2}$ があります。この円の中でマスを動かすゲームをします。
マスは最初 $(0,\ 0)$ にあり、ふたりはお互いのターンで $x,\ y$ 座標どちらかの正の向きにちょうど $k$ だけ進めます。円の外に出たら負けです。勝者は先手か後手か求めてください。
制約
$1\le d \le 10^{5}$
$1\le k \le 10^{5}$
考察・解法
ゲーム系の問題は苦手なので、実験して考察があまり進まない場合は Grundy 数を考えて、その定義から攻めるということを私はよくします。なので今回は Grundy 数を求める解です。1
まず、実験します。図は $d=8,\ k=1$ のときです。
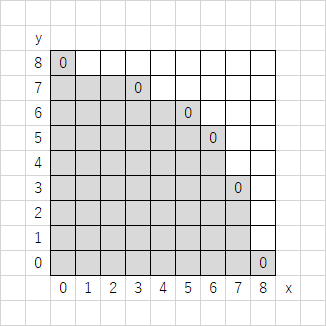
定義に沿って Grundy 数を求めます。図のように、右にも上にも行けないときは Grundy 数は $0$、つまり負けです。そうでない場合、右と上に遷移できるので、右と上にある数字の $\mathrm{mex}$ がその座標における Grundy 数です。
これに基づいて Grundy 数を埋めると、次のような状態になります。
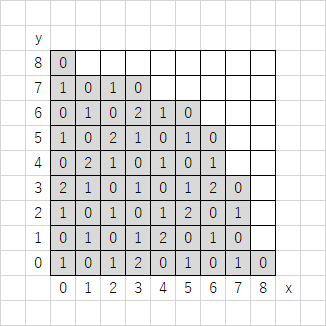
これをじーっと眺めると、$x-y$ が同じ場所は全て Grundy 数は同じということが分かります2。更に、直線 $x=y$ に対称なので、Grundy 数を全てのマスについて見る必要はなく、高々 $2d+1$ 箇所記録しておけば十分です。
これが分かれば、あとは $(0,\ 0)$ の Grundy 数が $0$ かどうかを見るだけです。
なお、$k$ の値が違う場合は盤面が違うだけで他は全て同じです。
実装
$x$ 座標が大きい方から順に見ます。盤面になりうるマスは $O(d^{2})$ 個ありますが、$x=y$ について対称なことを考慮すると $(0,\ 0)$ の Grundy 数が求まるまででよく、また $x-y$ が同じ座標では Grundy 数は同じことを考慮すると既に埋まっている場所を探索する必要もありません。そのため見る必要のあるマスは $O(d)$ 個であり十分間に合います。見る必要のあるマスは下図のような場所です。
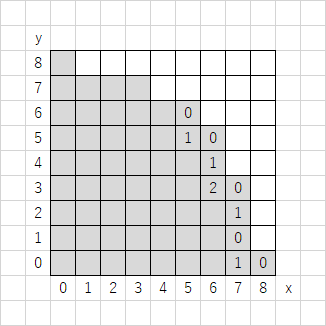
以下、私の C# による実装です。
実装を展開する
public static void Solve(Scanner cin)
{
int _t = cin.ReadInt();
for (int _i = 0; _i < _t; _i++)
{
var (d, k) = cin.ReadValue<int, int>();
var grundy = Enumerable.Repeat(-1, 2 * d + 1 + k).ToArray();
for (long i = d / k * k; (i + k) * (i + k) * 2 >= (long)d * d; i -= k)
{
long ok = 0;
long ng = 1000000000;
while (ng - ok > 1)
{
var mid = ok + (ng - ok) / 2;
if (i * i + mid * mid <= (long)d * d) ok = mid;
else ng = mid;
}
for (long p = ok / k * k; p >= 0; p -= k)
{
if (p == ok / k * k)
{
grundy[i - p + d] = 0;
continue;
}
if (grundy[i - p + d] != -1) break;
else
{
if (grundy[i - p + k + d] == -1)
{
grundy[i - p + d] = Math.Max(0, 1 - grundy[i - p - k + d]);
}
else grundy[i - p + d] = Mex(grundy[i - p + k + d], grundy[i - p - k + d]);
}
}
}
Console.WriteLine(Judge(grundy[d] == 1));
}
}
public static int Mex(int a, int b)
{
if (a == b)
{
if (a == 0) return 1;
else return 0;
}
return 3 - a - b;
}
public static string Judge(bool pred) => pred ? "Ashish" : "Utkarsh";
ACコード: https://codeforces.com/contest/1451/submission/99168943
感想
AC に1時間かかってしまいましたが、ゲーム系の問題もちゃんと AC できるようになっていて良かったです。ゲーム問題苦手だったので……。