エスパーです。正直こっちのほうが分かりやすいです。
厳密ではありませんが証明はちゃんとつけました。
問題リンク
https://atcoder.jp/contests/arc129/tasks/arc129_d
問題概要
長さ $N$ の整数列 $(A_1, \dots, A_N)$ があります。この整数列の両端は繋がっています。
$A_{i-1}, A_i, A_{i+1}$ にそれぞれ $-1,2,-1$ を何回か足すことによって $A_i$ を全て $0$ にできるか判定し、できるなら最小回数を求めて下さい。
制約
- $3\le N\le 200000$
- $-100\le A_i \le 100$
- 入力は全て整数
考察
今回は自分の解法を解説するので kmjp さんの解説と同じ内容は省きます。
行列を考えます。$i$ を選ぶ回数を $x_i$ とおくと、次のような関係が成り立ちます。
$\boldsymbol{A}=\boldsymbol{P}\boldsymbol{x}$
ただし、$\boldsymbol{A}=(A_1, A_2, \dots, A_N)^\top,\boldsymbol{x}=(x_1, x_2, \dots, x_N)^\top$。また、$\boldsymbol{P}$ は
\begin{pmatrix} -2 & 1 & 0 & \cdots & 0 & 1 \\ 1 & -2 & 1 & \cdots & 0 & 0 \\ 0 & 1 & -2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & -2 & 1 \\ 1 & 0 & 0 & \cdots & 1 & -2 \\ \end{pmatrix}
ここで、$\boldsymbol{P}$ の rank を調べると $N-1$ となります。つまり、$N-1$ 個の $x_i$ を決めれば残りの $1$ 個も決まります。
よって、適当な主小行列 (行列の $i$ 行目と $i$ 列目を同時になくした行列) の逆行列を考えたら上手に $x_i$ の値が決まりそうな雰囲気がします。
一方、設定から自明に $\sum A_i=0$ なので、rank が $N-1$ であることに由来する制約条件も分かるので、これは妥当な考察であることが分かります。
解法
先述の行列 $\boldsymbol{P}$ のうち $N$ 行目 $N$ 列目を取り除いた主小行列を $\boldsymbol{P’}$ とおきます。つまり、
\begin{pmatrix} -2 & 1 & 0 & \cdots & 0 \\ 1 & -2 & 1 & \cdots & 0 \\ 0 & 1 & -2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & -2 \\ \end{pmatrix}
です。また $\boldsymbol{A}, \boldsymbol{x}$ の第 $N$ 成分をなくしたものを $\boldsymbol{A’}, \boldsymbol{x’}$ とおきます。
$\boldsymbol{P}$ の rank は $N-1$ なので、$\boldsymbol{P’}$ は逆行列を持ち、$\boldsymbol{A’}$ が決まれば $\boldsymbol{x’}$ も一意に決まります。また、$\boldsymbol{x’}$ が定まれば連立方程式の適当などれか (例えば $x_N-2x_1+x_2=a_1$) を用いることで $x_N$ も定まります。
さて、$\boldsymbol{P’}^{-1}$ ですが、Wolfram Alpha に入れると次のようになります。これから、$(i, j)$ 成分 $(i\le j)$ が $\frac{-1}{N} i(N-j)$ である対称行列、つまり $(i, j)$ 成分は一般に $\frac{-1}{N} \min(i,j)(N-\max(i,j))$ である対称行列となることが推測されます。
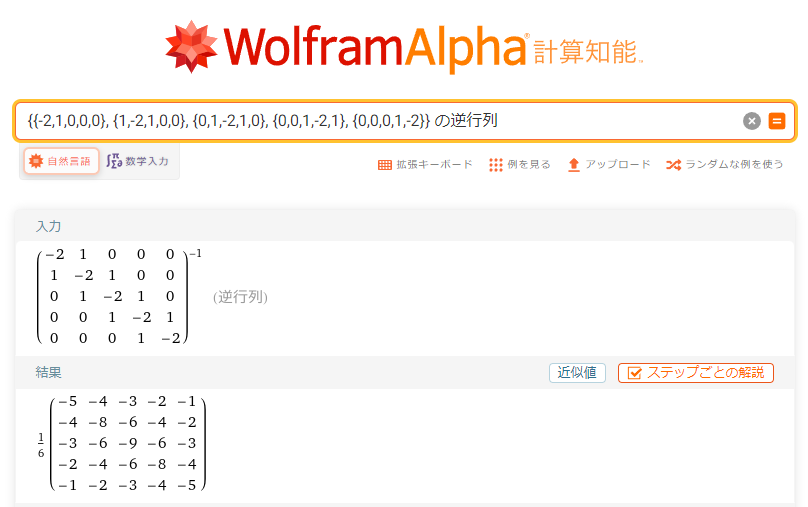
実際に $\boldsymbol{P’}^{-1}$ の各成分が $\frac{-1}{N} \min(i,j)(N-\max(i,j))$ であることは証明できます。
証明を展開する
$\boldsymbol{P'}^{-1}$ の 第 $(i, j)$ 成分 ($i, j$ のいずれかが $0,N$) を $0$ と仮定すると $\frac{-1}{N} \min(i,j)(N-\max(i,j))$ の自然な拡張となるので、そうします。$\boldsymbol{P’}^{-1}\boldsymbol{P’}$ の第 $(i,j)$ 成分を $c_{i,j}$ とおき ($1\le i,j\le N$)、これが $\delta_{i,j}$ に一致することを示します。ただし、$\delta_{i,j}$ はクロネッカーのデルタです。
$c_{i,j}=\frac{-1}{N} (\min(i-1,j)(N-\max(i-1,j))-2\min(i,j)(N-\max(i,j))+\min(i+1,j)(N-\max(i+1,j))$ と表せます。これは先においた仮定により成立します。
- $i=j$ のとき
$c_{i,j}=\frac{-1}{N} ( ( i-1)(N-i)-2i(N-i)+i(N-(i+1) )$ となり、これを展開して計算すると $c_{i,j}=1$。 - $i\lt j$ のとき
$c_{i,j}=\frac{-1}{N} ( ( i-1)(N-j)-2i(N-j)+(i+1)(N-j ) )$ となり、これを展開して計算すると $c_{i,j}=0$。 - $i\gt j$ のとき
対称性より自明。
以上より、$\boldsymbol{P’}^{-1}\boldsymbol{P’}=\boldsymbol{I}$、つまり両者を掛けると単位行列になるので題意が示された。
これにより、$\boldsymbol{P’}^{-1}$ が綺麗な形で計算できるので、累積和や Segment Tree などによって容易に $\boldsymbol{x’}=\boldsymbol{P’}^{-1}\boldsymbol{a’}$ を求めることができます。
ただし、これによって求めた解は負の値が含まれている可能性があります。全ての操作を同じ回数だけ増やしても連立方程式の解となるので、最小値が負の値なら $x_i$ を $x_i-\min{x}$ に置き換えます。これが求めるべき最小値です。
また、解が存在しない条件は、$\sum A_i=0$ でない、もしくは求めた $\boldsymbol{x}$ の値が整数とならないことです。
実装
実装を展開する
public override void Solve()
{
var n = sr.ReadInt();
var a = sr.ReadLongArray(n);
if (a.Sum() != 0)
{
Console.WriteLine(-1);
return;
}
var seg1 = new Segtree<long, Op>(a.Select((p, i) => -p * (n - i - 1)).ToArray());
var seg2 = new Segtree<long, Op>(a.Select((p, i) => -p * (i + 1)).ToArray());
var x = new long[n];
for (int i = 0; i < n - 1; i++)
{
x[i] += (i + 1) * seg1.Prod(i, n - 1);
x[i] += (n - 1 - i) * seg2.Prod(0, i);
if (x[i] % n != 0)
{
Console.WriteLine(-1);
return;
}
x[i] /= n;
}
x[n - 1] = 2 * x[0] - x[1] + a[0];
if (x[n - 1] % n != 0)
{
Console.WriteLine(-1);
return;
}
var min = Max(0, -x.Min());
for (int i = 0; i < n; i++)
{
x[i] += min;
}
Console.WriteLine(x.Sum());
}
public readonly struct Op : ISegtreeOperator<long>
{
public long Operate(long x, long y) => x + y;
public long Identity => 0L;
}
ACコード: https://atcoder.jp/contests/arc129/submissions/37407234
感想
なんでこれ通るんですか?感のある解答でした。ちゃんと証明したのでスッキリしました。ところで $\boldsymbol{x}$ の値が整数とならないことってあるんですかね……。