全完黄パフォ~~~!!!
ペナはもう少し縮まったはずなので反省も多いですが、最近の ABC は失敗ばかりだったのでとにかく嬉しいです!
問題リンク
https://atcoder.jp/contests/abc186/tasks/abc186_f
問題概要
縦 $H$ マス、横 $W$ マスのグリッドがあります。また、グリッド上には $M$ 個の障害物があり、$i$ 番目は $(X_i,\ Y_i)$ に置かれています。
障害物にぶつかるまで右または下にずっと移動できる飛車のコマがマス $(1,\ 1)$ にあります。飛車が $2$ 手で到達できるマスの数を求めてください。
制約
- $1\le H,\ W\le 2\times 10^5$
- $0\le M\le 2\times 10^5$
- $(X_i,\ Y_i)\neq (1,\ 1)$
- $(X_i,\ Y_i)$ は相異なる
考察・解法
$2$ 手で進む方法は、最初に右に進んで下に進むか、最初に下に進んで右に進むかのどちらかです。
例えば、進み方は下のように数えることができます。
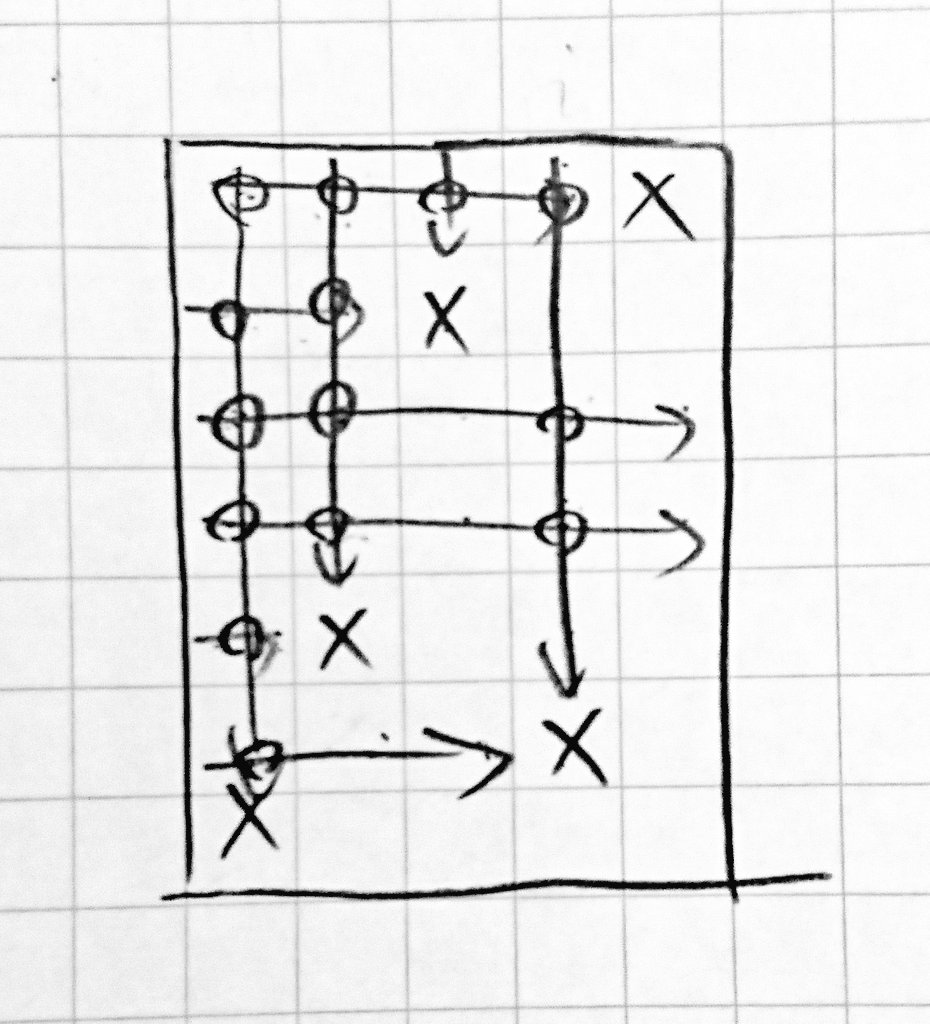
ここで、○を付けたマスは縦横どちらからも進めるマスです。
よって、進めるマス数 (縦横重複していてもいいので、矢印の通るマスの個数) から○のついたマス数を引く、という方針でいきます。
矢印の進める距離は、その縦・横の座標で最初にぶつかる障害物の位置として計算できます。
では、○を付けたマス数を数えましょう。例えば、図で左から $4$ 列目に注目します。
$4$ 列目からは $(1,\ 4)$ から $(5,\ 4)$ までの $5$ 個のマスに進めます。このうち、横に伸びる矢印でぶつかるのは横に伸びる行の $1,\ 2,\ \dots,\ 5$ (=縦の矢印の長さ) 個の矢印のうち、長さ $4$ (=今見ている列番号) 以上のものの個数です。
よって、縦に伸びる矢印の長さの小さいほうから順番に見ていき、multiset などに横に伸びる矢印を順次追加していくことで、横に伸びる矢印のうち列番号以上のものの個数を数えることができます。
【追記】最初に右か下に進むとき、$1$ 行目または $1$ 列目に障害物があるとそれよりも先の行・列は考慮してはいけないことに注意してください。
実装
実装を展開する
public void Solve()
{
var (h, w, m) = cin.ReadValue<int, int, int>();
var (x, y) = cin.ReadValueArray<int, int>(m);
var p = Enumerable.Zip(x, y, (x, y) => (x, y)).ToArray();
var yoko = Enumerable.Repeat((long)w, h).ToArray();
var tate = Enumerable.Repeat((long)h, w).ToArray();
for (var i = 0; i < m; i++)
{
yoko[x[i] - 1].Chmin(y[i] - 1);
tate[y[i] - 1].Chmin(x[i] - 1);
}
var yokoAvail = yoko[0];
var tateAvail = tate[0];
for (var i = tateAvail + 1; i < h; i++)
{
yoko[i] = 0;
}
for (var i = yokoAvail + 1; i < w; i++)
{
tate[i] = 0;
}
var tateS = tate.Select((value, index) => (value, index)).OrderBy(v => v.value).ToArray();
var yokoS = yoko.Select((value, index) => (value, index)).OrderBy(v => v.value).ToArray();
var ans = yoko.Sum() + tate.Sum();
var set = new Set<long>();
set.IsMultiSet = true;
int index = 0;
for (var i = 0; i < w; i++)
{
var next = tateS[i].value - 1;
if (next == -1) continue;
while (index < h && index <= next)
{
set.Add(yoko[index]);
index++;
}
var s = set.LowerBound(tateS[i].index + 1);
ans -= set.Count - s;
}
Console.WriteLine(ans);
}
ACコード: https://atcoder.jp/contests/abc186/submissions/18885562
感想
ABC の全完後の暇な時間で F 問題の解説を書くチャレンジ、成功!!!(わーい?)
時間かかりすぎたけど、とても嬉しいです!