今回はバチャでやった問題の反省文です。過去の ABC の問題の解説になります。

問題リンク

https://atcoder.jp/contests/abc161/tasks/abc161_e

問題概要

高橋さんは $N$ 日間のうち $K$ 日を選んで働くことにしました。

• 働く日どうしの間には $C$ 日以上空ける
• $S_i$ が x であるときは働かない。

これらの条件を満たすように働くとき、必ず働く日を全て求めてください。

制約

• $1\le N\le 2\times 10^5$
• $1\le K\le N$
• $0\le C\le N$
• 問題文の条件を満たすように働くことができる

考察

「必ず働く日」というのは、その日に働かないとどう頑張っても $K$ 日以上働くことはできないような日のことだと推測できます。
ここで、サンプル 1 を例にして考えてみます。

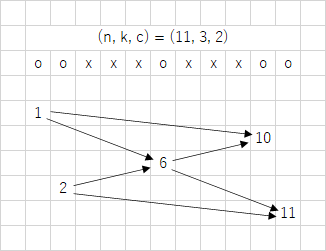
$i$ 日目を頂点、続いて働ける日を辺と考えたグラフにするとサンプル 1 は上のようになります。ここで、$K=3$ 日以上働けるような動き方は、$1,\ 2 \rightarrow 6\rightarrow 10,\ 11$ のように動くときです。この場合、必ず働く日は $6$ 日目です。

ここで、このような有向グラフの最長路問題は本質的に DP と等価な問題であることを思い出しましょう。DP でどうにかできないか考えます。
素直に各日付について何日目に働くかを DP してもよいですが、ここではあることに気付くと簡単に問題が解けます。条件の中で最大日数働こうとしたとき、どのように働いても $i$ 日目に働くのは最初から数えて $k$ 回目だとすると、$k$ は $i$ に関して一意に定まり、更に単調増加列を成します。
証明は簡単です。その日働くのが $k\pm 1$ 回目だとすると、前後で必ず働く回数が足りなくなるからです。
例えば、図の例で言うと、$1$ 日目に働く可能性のあるのは $[1,\ 2]$ 日に含まれる区間で、$2$ 日目に働く可能性のあるのは $[6,\ 6]$ 日に含まれる区間です。

以上より、$k$ 回目に働く可能性のある日付は区間を成します。この区間に含まれる働ける日が一意に定まるとき、その日付が答えです。

解法

$k$ 日目に働く可能性のある日付について DP します。$k$ 日目に働く可能性のある日付が区間 $[l_k,\ r_k]$ であるとするとき、$l_k,\ r_k$ はそれぞれ前と後ろから貪欲に (すなわち、前に働いた日から $C$ 日以上経過していれば割り当てるというような変遷を用いて) 日付を決めていくことで求められます。
ここで注意ですが、条件下で働くことの可能な最大日数が $K$ 日よりも真に多い場合は、任意の日に休んでも $K$ 日ちょうど働くことができるので答えはありません。

$l_k,\ r_k$ が求まれば、あとは $l_k=r_k$ を満たすような $l_k$ を全て出力すればよいです。

実装

		public void Solve()
		{
			var (n, k, c) = cin.ReadValue<int, int, int>();
			var s = cin.ReadString();
			var lLim = Enumerable.Repeat(-1, n + 1).ToArray();
			var rLim = Enumerable.Repeat(-1, n + 1).ToArray();
			int last = 0;
			for (var i = 0; i < n; i++)
			{
				if (s[i] == 'x') continue;
				if (last > 0 && i - lLim[last - 1] <= c) continue;
				lLim[last++] = i;
			}
			if (last != k) return;
			for (var i = n - 1; i >= 0; i--)
			{
				if (s[i] == 'x') continue;
				if (last < k && rLim[last] - i <= c) continue;
				rLim[--last] = i;
			}
			for (var i = 0; i < k + 1; i++)
			{
				if (lLim[i] != rLim[i]) continue;
				if (lLim[i] == -1) continue;
				Console.WriteLine(lLim[i] + 1);
			}
		}

ACコード: https://atcoder.jp/contests/abc161/submissions/19021632

感想

左右から見るのはドが付くほどの典型テクニックですが、今回は左右から見ることもその正当性にも気付かなかったので反省です。ちなみにバチャ本番ではそれぞれの日付に関してインライン DP の要領で左から割り当てていき、$K$ 日働く状態に到達不可能な日付を削除した後に、働く可能性のある日付が一意に定まる日付を全て出力したのですが、どこが嘘解法なのでしょうか。反例がまだ分かっていないので、分かった方はご教示頂ければ幸いです。

さて、AGC052 (Good Bye rng_58 Day 2) の裏でこの ABC バチャを走っていましたが、全完できずにまだスタートラインにも立てていないことが非常に悔しかったです。実力不足が故に rng_58 さんの最後の晴れ舞台に参加できなかったことは一生悔やむと思います (その AGC で善戦できたかどうかは別として)。
しかし、後悔はなんとやら、です。後悔するくらいなら努力して力を付けようと思います。来年の目標は AtCoder 黄色 (3 月まで¹)・橙色 (年内) に改めますので、全力で頑張ろうと思います。