Codeforces
解説記事や Editorial などをざっくり見ても自分の解法の解説が無かったので。
問題リンク
https://codeforces.com/contest/1380/problem/E
問題概要
$n$ 個の皿が $m$ 個のタワーに置かれています。皿は直径がそれぞれ $1,2,\dots,n$ であり、直径が $i$ である皿はタワー $t_i$ に置かれています。また、各タワーには上から直径が小さい順に皿が置かれています。
あなたは $m$ 個のタワーのうち $1$ つに全ての皿が乗っているようにしたいです。タワーは以下の操作を何回か行うことでまとめます。
- 好きな $i,j\ (1\le i,j\le m,\ i\ne j)$ を選ぶ。タワー $i$ から上から何個か (全部でも良い) の皿を取り、同じ順番でタワー $j$ の上に置く。このとき、動かす皿は全て操作前のタワー $j$ の一番上の皿よりも小さくてはならない。
タワーを $1$ つにまとめるのに必要な操作回数の最小値を、タワーをまとめる難易度と呼ぶことにします。
さて、$m-1$ 個のクエリ $a_i,b_i$ が与えられます。$i$ 個目のクエリはタワー $b_i$ の皿を全てタワー $a_i$ の皿とまとめ、新たなタワー $a_i$ にすることを意味します。新たなタワーも皿は上から小さい順になるようにします。これは難易度には関係しません。
全ての $k=0,1,2,\dots,m-1$ について、$k$ 番目のクエリまでを処理した状態でのタワーをまとめる難易度を求めてください。
制約
- $2\le m\le n\le 2\times 10^5$
- $1\le t_i\le m$
- $1,2,\dots,m$ までの整数がそれぞれ少なくとも 1 回以上 $t_i$ に現れる。
- $1\le a_i,b_i\le m,\ a_i\ne b_i$
- クエリ $a_i,b_i$ はどちらのタワーもそのクエリの時点で存在するようなものが与えられる。
謎制約。
問題リンク
https://codeforces.com/contest/1517/problem/D
問題概要
$n\times m$ のグリッドグラフが与えられます。$4$ 近傍で繋がっている各辺には道の長さが与えられています。
全ての $(i,j)$ について、$k$ 回移動を繰り返して最初の位置 $(i,j)$ に戻ってくるとき、移動経路の距離の最小値を答えてください。戻ってこれなければ -1 としてください。
制約
- $2\le n,m\le 500$
- $1\le k\le 20$
- $1\le (各辺の長さ)\le 10^6$
Educational Codeforces 初めての Unrated 参加でした。見事に出来ないといけない問題が解けずに Educate されました。
問題リンク
https://codeforces.com/contest/1473/problem/E
問題概要
$n$ 頂点 $m$ 辺の重み付き有向連結グラフが与えられます。ここで、二頂点間のパスの距離を、通る辺の重みの総和に、重みの最小値を足して、最大値を引いたものと定義します。頂点 $1$ から各頂点への距離の最小値を求めてください。
制約
- $2\le n\le 2\times 10^5$
- $1\le m\le 2\times 10^5$
- $1\le w_i\le 10^9$
あけましておめでとうございます!
本年の抱負は何事もなく無事進級すること、及び AtCoder 橙達成 (中間目標として 3 月までに黄色) です。今年もよろしくお願いいたします。
ID変更のご報告
Codeforces では毎年恒例のユーザー名変更が可能な時期となりましたので、AtCoder 及び Codeforces の ID を fancy_lettuce から fairy_lettuce に変更し、Topcoder 含め統一しました。
…C 問題は問題文が読みにくくて少しつらかったけど、D 問題も E 問題も面白くて楽しいセットでした。本番ギリギリ E が間に合わなくてつらかった……。
問題リンク
https://codeforces.com/contest/1469/problem/E
問題概要
ふたつの文字列 $a,\ b$ について、同じ位置に同じ文字が存在するような位置がひとつでもある場合、a bit similar といいます。
0 および 1 からなる文字列 $s$ について、その長さ $k$ の部分文字列全てと a bit similar である長さ $k$ の文字列のうち、辞書順最小のものを求めてください。そのような文字列が存在しない場合はその旨を報告してください。
制約
$1\le k\le n\le 10^6$
…この記事は、色変記事 Advent Calendar 2020 の12月9日公開の記事です。
色変記事アドベントカレンダー、なるものの募集を見ました。
色変記事AdventCalendarを作成しました。
— dokin (@ayoiyouyoeyo) November 4, 2020
みなさまの勇気ある宣言をお待ちしております!https://t.co/1NqMxq7Wu3
この恐ろしいアドベントカレンダーを見てしまった私。そういえば、AtCoder 青も Codeforces 紫も、近かったような……あれ、Topcoder も黄になれるんじゃ?
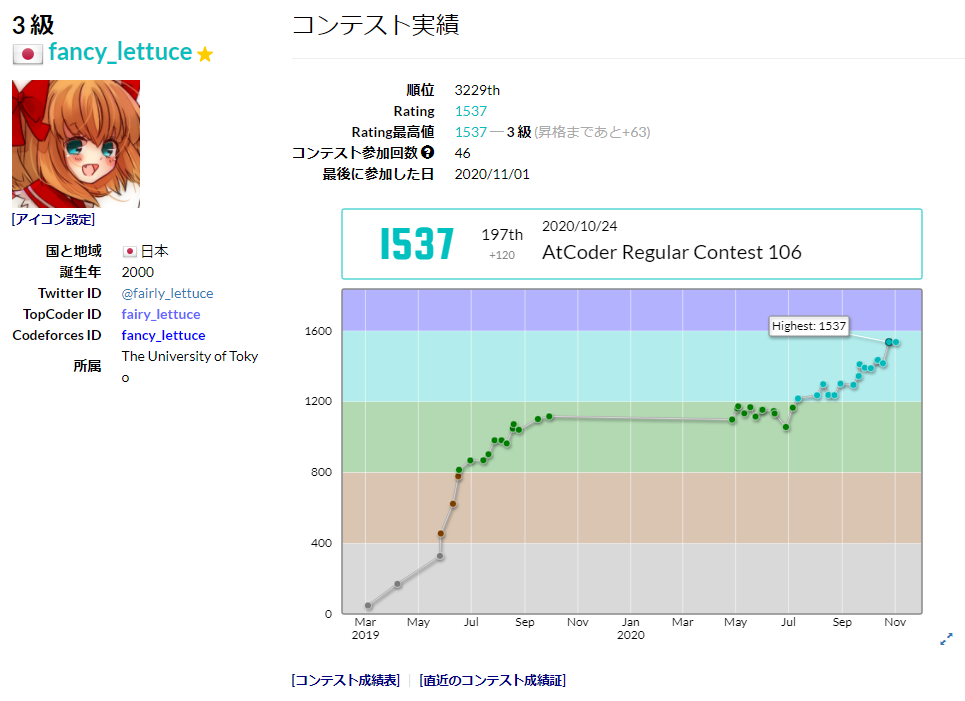
ということで、参加してみました。完全にノリですが、Topcoder はともかく AtCoder と Codeforces はずっと色変しないまま膠着していたので、これを期に色変してやろうと考えました。
(達成できたら)恐らく前代未聞の、3 コンテストサイト同時の色変記事になります。
…大爆死。反省を込めて解説ブログを書きます。
問題リンク
https://codeforces.com/contest/1455/problem/D
問題概要
非負整数からなる数列 ${a_i}$ および非負整数 $x$ が与えられます。
$a_{i}>x$ である $a_{i},\ x$ を swap することを任意の回数できます。$a$ を広義単調増加にするためには最小で何回の操作を行えばいいでしょうか。
制約
$1\le t\le 500$ (テストケース数)
$1\le n\le 500$
$0\le x,\ a_i\le 500$
これ E よりも簡単じゃないですか?
問題リンク
https://codeforces.com/contest/1454/problem/F
問題概要
$n$ 要素からなる数列 $a$ があります。$a$ を $1$ 以上の要素からなる $3$ つの部分列に分けます。
最初の部分列の最大値、真ん中の部分列の最小値、最後の部分列の最大値が全て等しくなるような分け方は存在しますか。存在するときはその分け方も出力してください。
制約
$1\le t\le 2\times 10^{4}$ (テストケース数)
$3\le n\le 2\times 10^{5}$
$1\le a_{i} \le 10^{9}$
$\sum{n}\le 2\times 10^{5}$
Div. 3 全完しようと思ったらこの問題に阻まれてしまいました。どう考えても不可能だと思ってたけど、よくよく見たらなもりグラフという制約を見逃していました。恥ずかしい。
問題リンク
https://codeforces.com/contest/1454/problem/E
問題概要
自己ループや多重辺のない $n$ 頂点 $n$ 辺の連結グラフ(つまり、なもりグラフ1)が与えられます。このグラフに含まれる長さが $1$ 以上の単純パスの数を求めてください。ただし、逆順にたどっただけのパスは同じものとみなします。
制約
$1\le t\le 2\times 10^{4}$ (テストケース数)
$3\le n\le 2\times 10^{5}$
$\sum{n}\le 2\times 10^{5}$
数列を当てる系のインタラクティブとても好きだし得意。この前の JOI の数当てもそうだったけど、こういう問題を考えるのがとても楽しいと思えます。
問題リンク
E1 (Easy Version): https://codeforces.com/contest/1451/problem/E1
E2 (Hard Version): https://codeforces.com/contest/1451/problem/E2
問題概要
$n$ 要素からなる数列 $a$ を当てるインタラクティブ問題。解答者はプログラムの中で以下の質問をすることができます。
AND i j: $a_{i}$ と $a_{j}$ の AND を質問する。OR i j: $a_{i}$ と $a_{j}$ の OR を質問する。XOR i j: $a_{i}$ と $a_{j}$ の XOR を質問する。
規定の回数以内の質問で元の数列を当ててください。
制約
$4\le n\le 2^{16}$
$n$ は $2$ の冪である
Easy: 質問の回数は $n+2$ 回以内
Hard: 質問の回数は $n+1$ 回以内